ТЕМА 05: ДОСТЪПНОСТ И ЛОКАЛИЗАЦИЯ

Досега локализационните модели интерпретират локализационния избор на фирмите на основата на двете икономически сили, които характеризират локализационните процеси – транспортни разходи (предизвикващи разсейване на дейностите) и агломерационни икономии (водещи до концентрация). С баланса между тези сили, моделите са в състояние да отчитат съществуването на агломерации на стопанските дейности при унифицирано пространство. В представените досега модели се демонстрира логиката, която определя пазарните зони при конкретна пространствена структура на търсенето, производство се развива в конкретни точки в пространството и така създава отдалечени пазари.

5.1. Достъпност и транспортни разходи.

Теориите разглеждани в настоящата тема променят досега представените постановки за пространствена структура на търсенето и предлагането. Мястото на производството в моделите, които ще бъдат разгледани вече предполага неговото пространствено измерение, а мястото на потреблението (пазара) е точково.

Тази обратна постановка в условията на тези модели е свързана с проблема, който тези модели си поставят за решаване. Моделите досега стигнаха до идентифициране на пазарните зони на всеки производител. Но има и друг въпрос, който все още не е разгледан – как да се определи „производствената зона” (териториалния обхват на производството), имайки предвид физическото пространство (земята), която се заема от отделните стопански дейности. В теориите, даващи отговор на този въпрос локализационните решения са продиктувани от един основен принцип на пространствената организация на всяка дейност, а именно „принципа на достъпността” до даден пазар или „център”. За фирмите, висока достъпност означава, че те имат лесен достъп до широк и диверсифициран пазар на стоки, производствени фактори, информация, както и до центрове на международни инфраструктури.[1] За хората, т.е. за нуждите на бита, достъпността означава достъп до „централен бизнес район”, а следователно и до работни места. Това означава, че техните комуникационни и пътни разходите са минимални, като в същото време те имат лесен достъп до широк спектър от други услуги, ограничени до определени места (например театри, музеи, библиотеки) и близост до специфични услуги (например университети), без да се налага да плащат високи разходите за пътуване (на дълги разстояния).

Високото търсене на достъп до централни зони води до конкуренция между промишлени и битови дейности, за локализация по-близка до пазара, или по-общо казано, по-близо до хипотетичен бизнес район (или физически център на града).

Всички локализационни модели, описани в този раздел имат важен общ елемент – разходи за закупуване или наемане на земя. Ако приемем, че съществува един основен бизнес район, поради голямото търсене на места с минимални транспортни разходи, земята близо до този притегателен център ще струва повече, защото е създадено едно относително постоянно общо предлагането на ресурса градска земя, в краткосрочен и средносрочен период. При тези модели конкуренцията се проявява на базата на строгия икономически принцип – фирмите, които успяват да се настанят в притегателния бизнес район са онези, които могат да плащат по-високи наеми.

За разлика от теориите за локализацията на икономическите дейности (напр. по модела на Weber), които предвиждат локализационни решения основани не само на минимални разходи за транспорт, но и в съответствие с очаквани агломерационни икономии, то разглежданите в настоящата тема модели предвиждат само един фактор организиращ дейността в пространството – разходите (наема) за земята, като това е единственият принцип, който обяснява локализационните решения на всички видове дейности (селско стопанство, друг вид производство или битови дейности).

Това е и силата на тези модели – логиката, с която те отразяват разпределението на производствените (вкл. селскостопанските) и битови дейности в географското пространство, отчитайки единствено физическо разстояние от притегателния център (бизнес, градски и т.н.). Като се има предвид структурата на търсенето и предлагането в пространството, то този вид модели са особено подходящи за анализ на локализацията на производствените и битови дейности в градското пространство. Според т.нар урбанизационна икономика, е лесно да се предположи съществуването на един бизнес район (град, център), който за фирмите изпълнява функция да събира, разпространява и изнася произведените продукти, а за домакинствата е място, където се намират работни места и други институции. Затова тези модели са в състояние да установят локализацията на отделна фирма или домакинство спрямо един притегателен център.

Първият модел, анализиращ пространственото разпределение на алтернативни производствени дейности, е разработен в началото на деветнадесети век от Johann Heinrich von Thünen (снимка) (1783-1850)

През 60-те години на 20-ти век проучвания правят още Walter Isard (снимка), Martin Beckmann and Lowdon Wingo, които подготвят основата за формулировката направена от William Alonso по прилагане модела на Von Thünen към градската среда – „моделът на моноцентричния град”. В тази тема първо ще бъде представен модела на Thünen, който по прост начин и със строга икономическа логика обяснява пространственото разпределение на селскостопанското производство около един град. След това ще се представят модели разработени върху същата теоретична основа, за да се изследва локализацията на фирмите и домакинствата в градските райони. Този модел се превръща в самостоятелна школа в рамките на локализационната теория, известна като „нова урбанистична икономика”. Стремежът е да се разработят общи модели за локализационно равновесие, в които основният интерес вече не е локализационното решение на отделната фирма или домакинство. Вместо това, основни области на проучване стават определянето на размера и плътността на населените места и разработване на модел за разходите за земята при различни разстояния от града, така че да се гарантира постигането на локализационно равновесие за всички физически лица и фирми в града. Както ще видим, тези теории създават модели, доказващи икономическия характер на пространствените явления и показващи, че те могат да бъдат анализирани с традиционните инструменти на икономическата теория. Те са всъщност приложение на микроикономическата теория при изследване на вътреградската структура.

5.2. Локализация на селскостопанските дейности. Модел на Johann Heinrich von Thünen

Johann Heinrich von Thünen разработва първия локализационен модел основан на непрекъснатото производствено пространство и точков пазар на произведената продукция.

Моделът на von Thünen за разпределение на земеделската дейност около един град се основава на приемания, които следващи теории също прилагат:

- налице е унифицирано пространство, където цялата земя има едно и също плодородие и транспортната инфраструктура е еднаква във всички посоки (изотропно пространство);

- има само един център (град), където се търгуват всички стоки (т.е. известна е точковата локализация на пазара);

- приема се, че търсенето на стоки е неограничено, т.е. локализационното равновесие зависи от условията на предлагането;

- факторите на производството са съвършено разпределени в пространството – разпределението на земята между отделните производствени дейности не зависи от пространственото разпределение на другите производствени фактори;

- налице е производствена функция с постоянни коефициенти и постоянна възвръщаемост от мащаба при всяка земеделска продукция – това предположение означава, че количеството на получената продукция от всяка поземлена единица и разходи за единица продукция, са постоянни в пространството;

- съществува съвършена конкуренция на пазара на земеделски стоки – земеделските стопани приемат за даденост цените на стоките, които произвеждат;

- единичните транспортни разходи са постоянни в пространството – общите транспортни разходи зависят от разстоянието между мястото на производство и града, и от обема на производство; транспортни разходи могат да варират в зависимост от реколтата.

Ако приемем, че съществуват определен брой земеделски производители, von Thünen отнася проблема до това как да се разпредели земята между земеделските производители, работещи в района около мястото на пазара.

Той основава своя модел на:

• Теория за оферираната рента – наемът (рентата) се разглежда като остатъчна величина, което е характерно и за следващите модели – това, което фермерите са готови да заплатят за земята е остатъчна стойност, след като транспортните и производствени разходи, включително и някакво възнаграждение (печалба) за фермера, се приспаднат от приходите.
• Въпроса: Как ще се разпредели земята между земеделските производители, работещи в района около мястото на пазара (моноцентричния град)?

Във формален смисъл, ако х е количеството на една стока, произведена от един земеделски стопанин, с е себестойността на единица продукция, р е цената на стоката, τ е разхода за единица разстояние за транспорта на единица продукция, и d е разстоянието до пазара, наемът за земята r се определя така:

 (5.1)

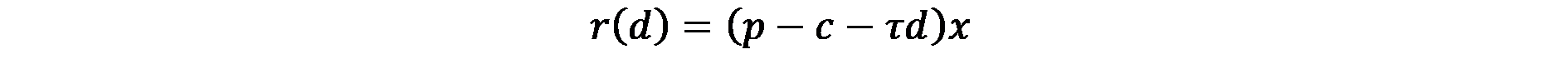
Това уравнение обяснява равнището на рентата (наема), който земеделските производители са готови да платят за земя на различни разстояния от пазара, където се търгуват стоки. Той е представен от права линия, с наклон – τd и пресечни линии равни на (p – c)х и (р – с)/τ, съответно показващи максималната стойност на наема (който е в точката на пазара – града) и максималното разстояние от града, където стойността на земята е нула.

От горното уравнение може да се получи промяна на наемите в пространството (например от един километър) чрез изчисляване на първата производна на наема по отношение на разстоянието:

 (5.2)

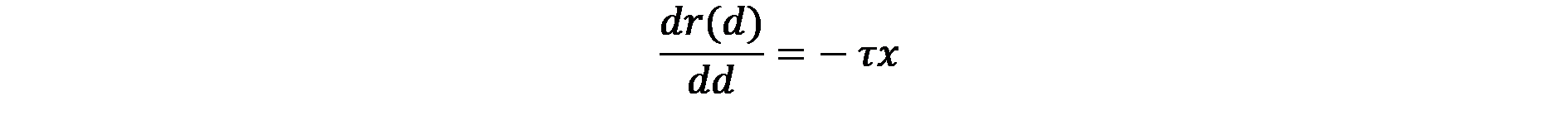
Както уравнението показва, разликата в наемите е точно равна на „- τx” .

Това означава, че по-близкото разстояние до центъра води до:

увеличение на наема свързано със заемане на по-централна локализация

=

спестяване на общите разходи (заради намаление на транспортните разходи)

Спестяванията в общите разходи за транспорт при по-близка локализация до центъра са равни на увеличение на наема свързано със заемане на по-централна локализация.

Пример:

Трима земеделски производители (A, B и C), всеки от тях произвежда специфичен земеделски продукт, с различна степен на трайност, за всеки земеделски производител се построява крива за рентата (наема) за земя. Тъй като стоките имат различна степен на трайност, кривите за поземлената рента имат различни позиции и наклони (фигура 5.1). Земеделският производител, който произвежда най-нетрайна стока ще има производствен процес, който използва земята по най-интензивен и икономически ефективен начин (геометрично това е най-високата пресечка на ординатата, равно на (p – c)х, и той ще бъде по-склонен да плати висок наем за земя, за да бъде по-близо до града (геометрично, по-стръмен наклон на правата линия, равен на – τx).

Тъй като земеделските производители се конкурират за по-достъпна до пазара земя, всяка единица площ ще бъде предоставена на земеделски производител, готов да плати най-висок наем за тази земя.

Що се отнася до a', земята ще бъде дадена на земеделски стопанин А, който предлага най-висок наем за най-централните места. От a' до точка b’, земята ще бъде за фермер B, а от b’ до с’ на земеделските стопанин C. Действителният наем реализиран от собственика на земята в резултат на обработването на земята му е форма, получена от трите криви на предлагания наем.

Едно от основните предимства на този модел е способността му да докаже, че разстоянието, или достъпността до пазара (града) (изразено чрез транспортните разходи), е причина за разликите в поземлената рента. По този начин този модел се различава от класическото разбиране на Рикардо, че разликите в рентабилността на земята се дължат на различното плодородие. По този начин този модел може косвено да обясни локализацията на стопанска дейност в пространството – резултат, който е значимо постижение.

Фигура 5.1 Разпределение на земята между трима земеделски производители. Модел на Heinrich von Thünen

5.3. Градска локализация на фирмите. Модел на William Alonso

В началото на 1960-те години на 20-ти век William Alonso, а след това и Richard Muth преразглеждат модела на Von Thünen и го адаптират към градската среда, като по този начин проправят пътя за множество последващи изследвания. Alonso и Muth разширяват основата на модел на Thünen, като го правят от една страна по-приложим за градските условия, но те също го правят и по-общ като считат, че транспортните разходи са израз на пространствени ограничения и на предпочитанията за по-централна локализация.

Предположенията на модел на Alonso са същите като тези на модела на Thünen за селскостопанските дейностите, описан по-горе. Той обаче разглежда един град (вече не е околоградски район), който се характеризира с унифицирано пространство (хомогенно пространствено разпределение на производствените фактори) и с инфраструктура, която обхваща целия град във всички посоки (изотропно пространство). Градът има един център (бизнес район), който е определен като най-привлекателното място за всички фирми и домакинства. Като се имат предвид тези предположения, се прави анализ само на едно измерение – радиус включващ различните разстояния от центъра на града към периферията

Базовият модел се занимава с проблем, подобен на този, с който се занимава Thünen. Тъй като фирмите се конкурират за централните места, моделът показва по какъв начин градското пространство се разпределя между алтернативни видове дейности, след като се знае пазарната стойност на земята на различни разстояния от центъра.

Също така, моделът на Alonso определя наема като остатък след като предприемачът приспадне производствените разходи (включително и транспортните разходи) и желаното ниво на печалба от приходите, получени от продажбата на стоката. Формално наемът се изразява така:

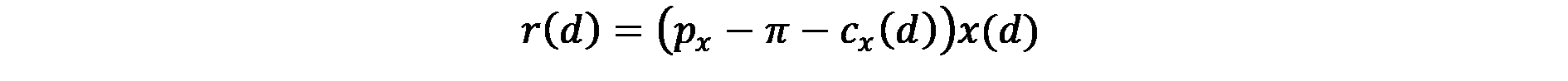
 (5.3)

където r показва единичния наем, p_х цената за единица произведена продукция, c_x разходите за единица продукция (включително транспортни разходи), π печалбата, d разстоянието от центъра и х е количеството на произведената стока.

Тъй като производствените разходи включват транспортните разходи, в модела на Alonso те зависят от разстоянието, както при модела на Thünen. Въпреки това, за разлика от модела на Thünen, приходите също зависят от разстоянието – по-голямата близост на крайградската локализация дава по-голяма близост до по-широките пазари, следователно достъп до по-високи доходи (например продажбите на магазин, разположени в центъра на града са по-големи в сравнение с тези в периферията, особено ако те продават луксозни стоки).

Уравнението изразява оферирания наем (на кв. м), който предприемачът е готов да плати при различни разстояния от центъра, след като разходите и печалбата на предприемача са приспаднати от приходите. Печалбите остават едни и същи, по-централно място означава готовност да се плаща висок наем, защото предприемачът има по-ниски транспортни разходи и получава по-високи приходи. По същия начин, крайградско място може да осигури същата печалба, само ако се плаща по-малък наем за земята – спестеното от разходи за земята ще трябва да компенсира по-високите транспортни разходи и по-ниски приходи, като резултат от по-нецентралното местоположение (фигура 5.2-a).

Наклонът на кривата за оферирания наем на земята, която изразява варирането в разходите за земя в резултат на единица изменение на разстоянието от центъра се изчислява по формулата:

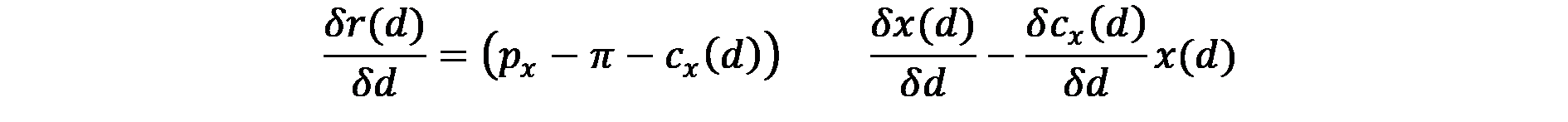
 (5.4)

Това показва, че на един км по-далеч от центъра, наемът при запазване на същото ниво на печалба, намалява поради увеличението на разходи за транспорт и намаляването на приходите.

На всяко разстоянието от центъра (например d₀ на фигура 5.2-b), ако фирмата иска да увеличи печалбите си, тя трябва да плати по-нисък наем. Но за същото разстояние, фирмата може да предложи и по-висок наем, ако е склонна да получава по-ниски печалби. Следователно е възможно да се построят различни криви за рентата на отделната фирма, всички с еднакъв наклон, всяка определена на базата на различно ниво на печалбата, което нараства с приближаването към изходната точка.

В рамките на едно частично равновесие, което предполага „пазарна крива на поземлената рента” (т.е. реалните пазарни разходи за земята – крива r на фигура 5.2-b), е възможно да се определи оптималната локализация за фирмата. По протежение на пазарата крива на поземлената рента (r), фирмата ще избере локализация, която носи най-голяма печалба, което е изразено чрез допирателната на пазарната крива на рентата с кривата на най-ниската оферирана рента. На фигура 5.2-b локализационното равновесие се достига в точка Е – това е разстояние d₀ от центъра и при рента равна на r₀.

Накрая, в един пример с три фирми, работещи в сектори, за които централното местоположение е с различна значимост (например моден бутик, търговец на дребно на компютърна техника и хлебарски магазин), е възможно да се определят за всеки от тях кривата на наема, чието разположение и наклон са различни, защото продажбите на фирмата имат по-голяма или по-малка чувствителност към централно местоположение. Следвайки точно модела на Thünen, трите фирми се подреждат на земи от градски район, според тяхната готовност да плащат – на всяко разстояние от центъра, на фирмата готова да плати най-висок наем, ще се даде да използва земята (фигура 5.2-c).

Има още един интересен аспект. Разликата в „плодородието” на различни видове земя традиционно се възприема като определящо за различията в поземлената рента. В този модел може да се тълкува в съвременния смисъл на градската икономика, като различна „производителност” на по-централната градска земя, поради по-големия достъп до информация. Ако приходите и разходите варират в зависимост от разстоянието, наемът е стойността, която намалява всички нетни приходи до такива, получени от граничните земи.

5.4. Разположение на домакинствата в градовете

Моделът за домакинствата, формулиран от William Alonso, е изцяло подобен по своята теоретична основа и аналитична структура на модела представен за фирмите. В този модел, локализационният избор вече не се прави от фирми, а от домакинства. Основната разлика от модела на Alonso за фирмите е влиянието върху избора на една нова променлива – големината на жилището (къщата). Едно домакинство може на практика да реши да се откаже от жилищно пространство с цел да се приближи към центъра на града. Икономията, получена от закупуване (наемане) на по-малко жилище, и от по-ниските транспортни разходи, свързани с по-централното местоположение, дават възможност на домакинствата да плащат по-високи разходи за единица земя.

Моделът за домакинствата се състои от три променливи: разходите за земята (или за къщата), големината на къщата, и транспортните разходи.

Да приемем следната функция на полезност за домакинството:

 (5.5)

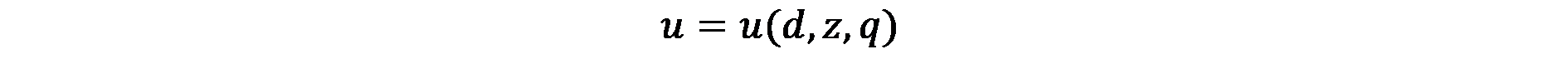
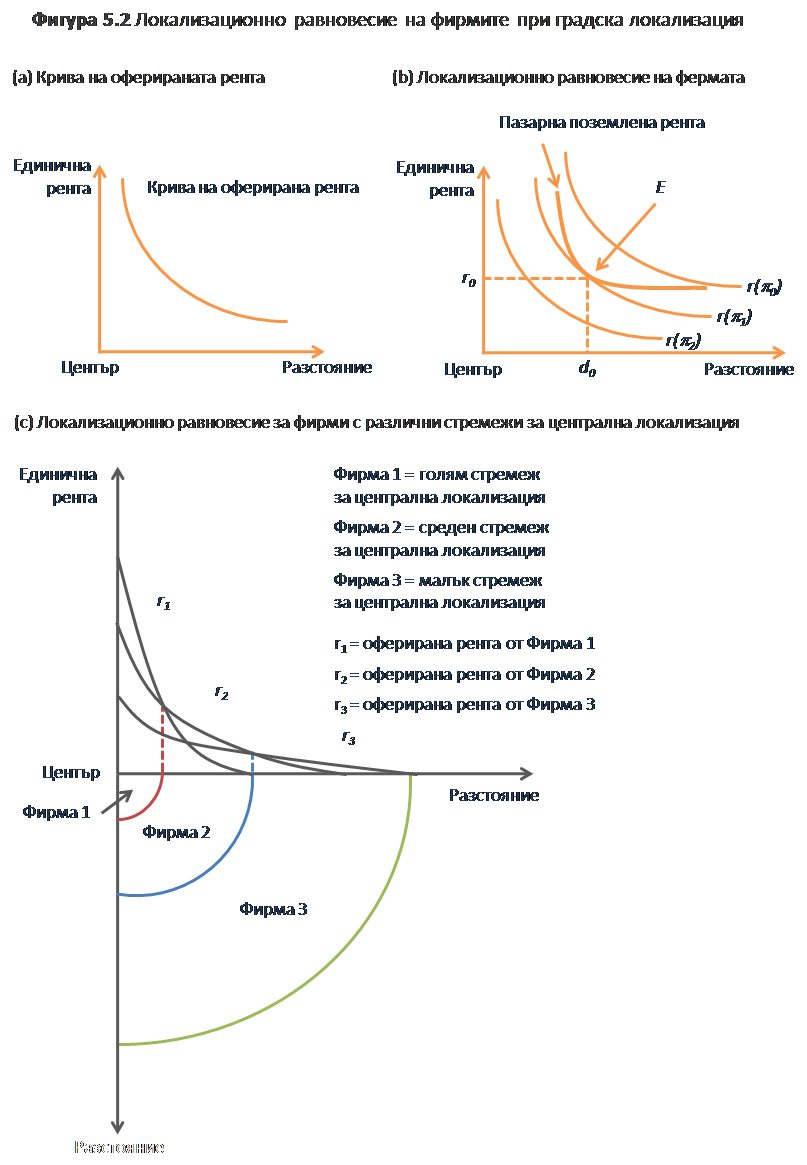
където d е разстоянието от центъра на града, q е размерa на къщата, и z са всички други блага, от които домакинството се нуждае.

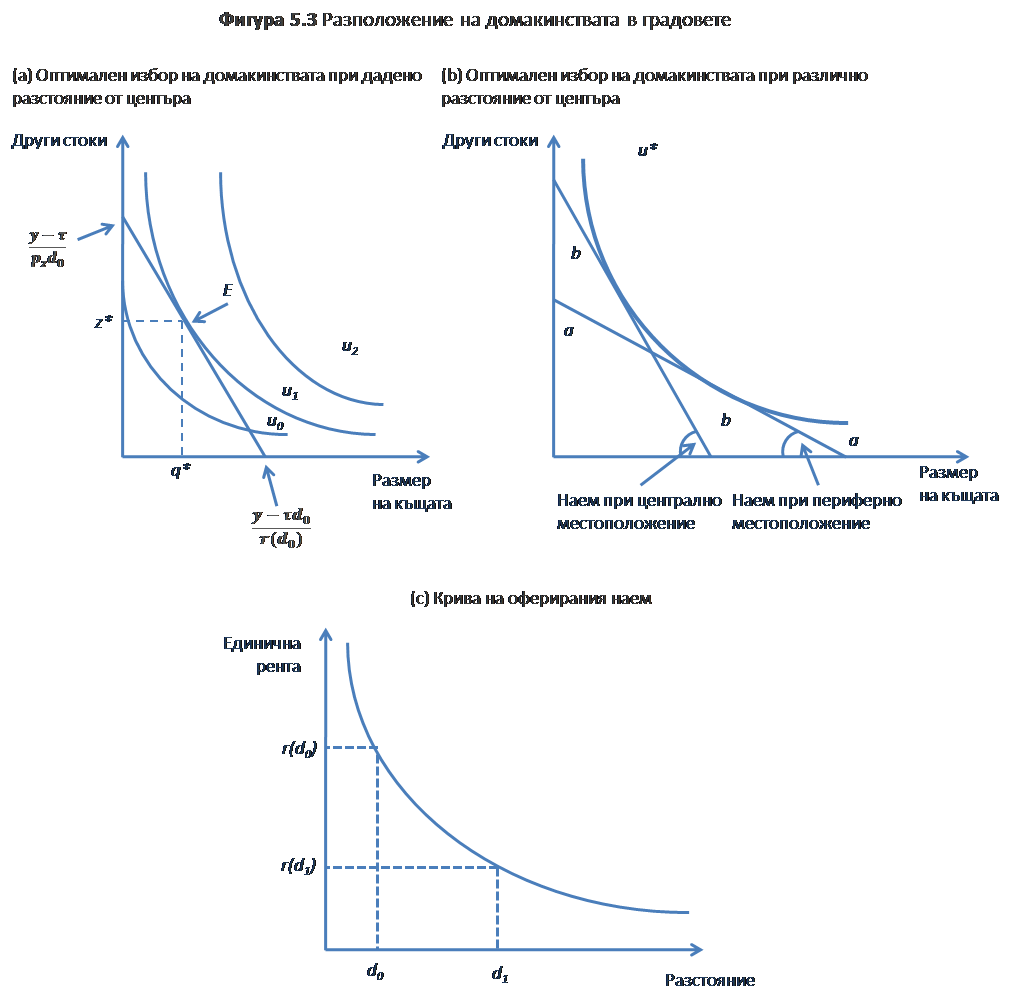
При дадено разстояние от центъра и каква да е комбинация между размера на къщата, размера q и другите блага z, всяко намаляване (дори леко) в размер на къщата води до загуба на удовлетворение за домакинствата, което трябва да се компенсира – за да се запази общата полезност – чрез увеличаване на количеството на другите блага, притежавани от домакинството. Това условие е изобразено на фигура от 5.3-a, което показва така наречените криви на безразличие (индиферентни криви) за различните комбинации „размер на къщата/ количество други блага”, които осигуряват една и съща полезност за домакинството. Всяка крива на безразличие представлява определено ниво на полезност, което се увеличава с увеличаване на разстоянието от началото на координатната система. Домакинството ще се стреми да се позиционира в най-високата крива на безразличие, при съобразяване с бюджетните ограничения, т.е доход равен на разходите, които трябва да извършва. Бюджетното ограничение се представя като:

 (5.6)

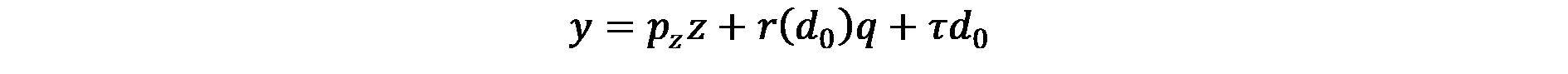
където у е домакинския доход, r(d₀)q и τd₀ са съответно разходите за къщата и за транспортните разходи на разстояние d₀, а p_zz представлява разходите за закупуване на други блага. При решаване уравнение 5.6 за z, получаваме:

 (5.7)

Графично, бюджетното ограничение се представя с права линия с отрязък (y – τd₀)/r(d₀), ако домакинството реши да похарчи целия си доход за къщата, а не за закупуване на други блага, както и (y – rd₀)/p_z,, когато домакинствата решат да използва целия си доход за закупуване на други блага.

Условието, при което се максимизира полезността на домакинството, в рамките на бюджетното ограничение, се представя от точката на допиране между бюджетната линия и кривата на безразличие. Домакинството не може да премине това ниво на полезност, тъй като не разполага с доход, за да го направи, като в същото време, е нерационално за домакинството да се позиционира под това ниво на полезност, при положение, че има доходите за това (фигура 5.3-а).

Математически, това условие се изпълнява ако наклонът на двете криви е един и същ:

(5.8)

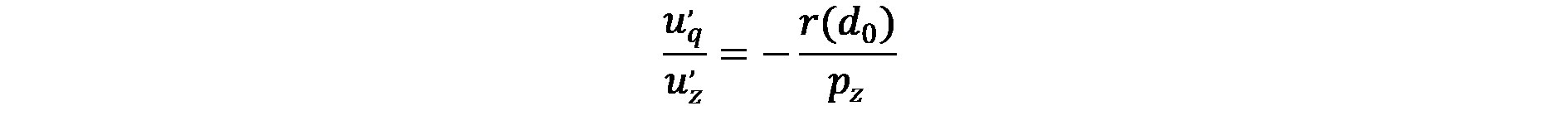
Ако приемем, че благото z се изразява в мерна единица – т.е. цената е равна на единица – наклонът на бюджетната линия е точно равна на наема r(d₀). Уравнението показва, че в равновесие, домакинството е безразлично към заместване на другите блага с площ от къщата, когато относителната полезност, произтичащи от тях (u_q^’/u_з^’) е равна на наема. Всяко домакинство, по този начин изразява, че максималната сума, която може да плати за всяко разстояние от центъра съответства на определено ниво на полезност, която желае да постигне (u* на фигура 5.3-b). За да изрази домакинството по-малко търсене на благото „къща” (т.е. приема по-малка къща) и да похарчи доходите си за други блага, при постоянна полезност, цената на къщата трябва да се увеличава. Така другите стоки стават относително по-евтини и следователно относително по-привлекателни за потребителите. На фигура 5.3-b, за да останат домакинствата на същата крива на безразличие, бюджетното ограничение трябва да има наклон bb линия.

Стъпка напред е да определим самия наем – при определено ниво на полезност, можем да изразим различни наклони на бюджетната крива при различни разстояния от центъра. С намаляване разстоянието до центъра, бюджетната линия става по-стръмна, благодарение на увеличение на максималната рента предлагана за разстояние, посочено на фигура 5.3-c.

Анализът дава следния важен резултат – кривите на съответните наеми са просто трансформация на кривите на безразличие в пространството на потреблението (компромис между благата z и размер на къщата q от фигура 5.3-b) в съответни криви на безразличие в градското пространство (компромис между наема и разстоянието от фигура 5.3-c).

Наклонът на кривата на наема спрямо разстоянието изразява увеличение на единичната цена на земята (на къщата), която домакинството е готово да поддържа, за да се придвижи по-близо до център, като запазва общата полезност постоянна. Това кореспондира с:

 (5.9)

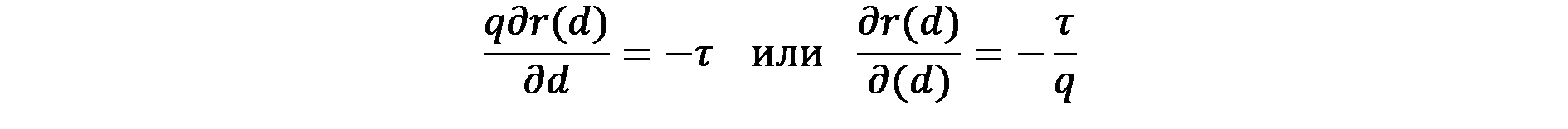
Уравнението известно като ”условие на Muth”, определя безразличието към алтернативни локализации чрез посочване на условието, при което алтернативните локализации поддържат полезността за домакинството постоянна. В действителност, това уравнение е като уравнението в модела на Thünen, като единствената разлика е само от включването на допълнителната променлива – размера на къщата (q), който намалява при движението към центъра, тъй като физическото пространство става по-скъпо. В този случай, домакинството е безразлично към по-малко периферни местоположения, когато икономията от по-ниски транспортни разходи и закупуване на по-малка къща е равна на по-високи единични разходи за земята от централните места. Формата на кривата на наема следователно не е линейна, а експоненциална (както при Thünen), при все още отрицателен наклон.

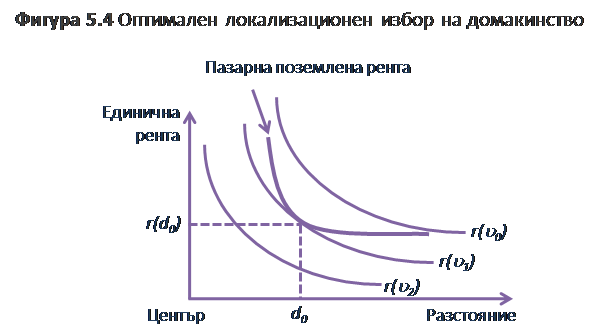
Както и в случая с фирмите, локализационното равновесие се получава от обединяването на пазарната крива на поземлената рента (реалните пазарни цени на земята, определени екзогенно) на кривите на оферираната рента. Точката на допиране между реалната крива на наема и най-ниската оферирана рента (отнесена към най-високата полезност) представлява оптималния локализационен избор на домакинството (Фигура 5.4).

 

Интересен елемент на анализа е ефектите от нарастване на дохода на домакинството при локализационното равновесие. Да вземем като даден размера на къщата. Домакинството ще избере място на такова разстояние от центъра, където по-нататъшно преместване към периферията (разходите за транспорт с на фигура 5.5-a) ще се изравни с пределното предимство (спестяванията от разходи за земя (υ на фигура 5.5-a). Увеличаването на доходите може да доведе до обратно решение за преместване – ако домакинството е по-заинтересовано от по-голям размер на къщата, предимството от спестяване при цената на къщата се увеличава (крива v се премества към v’ на фигура 5.5-b) и домакинството ще избере по-периферен район. Когато домакинството е заинтересовано от по-големи алтернативни разходите за транспорт (крива с минава към с’ на фигура 5.5-b), то ще избере по-централни местоположения. В присъствието на двата ефекта, по правило се счита, че първото (големината на къща) има определяща роля, в резултат на което локализационното равновесие се измества към периферията.