ТЕМА 06: ЛОКАЛИЗАЦИОННИ ФАКТОРИ. МОДЕЛИ НА ОБЩОТО РАВНОВЕСИЕ

 

С натрупването на концепции и модели за локализационно решение на фирмите е важно да се представят и съвременните разбирания за процеса на вземане на решения свързани с избор за местоположение на икономическите субекти. В настоящата тема се прави и кратка дискусия на моделите за общото равновесие, тъй като те представляват един от най-важните раздели на урбанистичната икономика след 80-те години на 20-ти век.

6.1. Локализационни фактори и решения

Локализационните фактори можем да групираме в две основни групи: териториални и извънтериториални.

Териториални (регионални, местни, преки) фактори:

-   Природни условия и географско положение,

-   Материално-веществени ресурси

-   Население (трудови ресурси)

-   Потреблението и свързаните с него транспортни разходи

-   Степен на изграденост на инфраструктурата (техническа, социална, публични институции)

-   Отпадъци (опазване на околната среда и здравето на хората)

Взаимодействието между обекта на локализация и територията се изразява от една страна във въздействие на фирмата (предприятието) върху територията и от друга – във функции на територията върху локализирания обект:

Обектът въздейства върху територията чрез следните функции:

-   Произвежда стоки и/или услуги

-   Изчерпва ресурси

-   Осигурява заетост

-   Въздейства върху миграцията

-   Променя екологичната обстановка

-   Въздейства върху развитието на територията

От своя страна територията въздейства върху локализираните върху нея обекти чрез:

-       Задоволява потребности на предприятието

-        Лимитира количеството и качеството на потребяваните ресурси

-        Осигурява потребление (пазар) на продукцията

-        Осигурява възпроизводствена среда за заетото в предприятието население.

Втората група локализационни фактори са т.нар. извънтериториални (косвени) фактори. Към тях могат да се причислят:

- Научно-технически прогрес

- Обществена организация на производството

- Стратегически решения

- Международни икономически отношения

- Времевата динамика и др.

Съвременното измерване влиянието на локализационните фактори се извършва основно чрез прилагане на факторен анализ: определя се индивидуалното и комплексно влияние на факторите. Самата технология на анализа включва: набиране на изходна информация; качествен анализ на събраната информация и подготовка на матрица на регионалната информация; подготовка за електронна обработка; обработка на данните; представяне на резултатите; прогноза за промени

Икономическата обосновка на локализационни решения преминава през предварителна оценка за ефекта на локализация.

Етапи на предварителната оценка включват:

1.   Определяне на териториалната единица за локализация

1.1. Определяне на ресурсната осигуреност по отношение на вид, обем, структура и възможности за експлоатация на природните ресурси (земя, вода, минерални суровини, енергия и др.)

1.2. Характеристика и оценка на равнището на специализация и концентрация

1.3. Отчитане на насоките за развитие на териториалната единица (според програмни документи)

1.3. Оценка за състоянието на: работната сила, техническа и социална инфраструктура, среда и др.

1.4. Определяне на характера, интензитета и ефективността на вътретериториални и междутериториални производствени връзки

2. Определяне на конкретен локализационен пункт

2.1. Оценка на земята

2.2. Геоложка характеристика (релеф, почвен слой, воден слой и др.)

2.3. Икономическа характеристика на местоположението – близост до източници на ел.енергия, ВиК, транспортни връзки, разходи за тяхното доизграждане и цялостен достъп

2.4. Оценка за наличие на съседни обекти (с възможност за комбиниране или конкуриране)

Критерии за локализационен избор

Локализационните фактори, за да получат количествена оценка, е необходимо да бъдат представени чрез система от показатели.

Критерии – стойности на показатели за локализационен избор, даващи количествена оценка на локализационните фактори (под формата основно на разходи)

Системата от критерии, които се избират трябва да имат следните характеристики: всеобхватност, действеност, разложимост, недвусмисленост, концентрираност, устойчивост

Възможните вариантите за локализация на даден обект се оценяват или само на основата на транспортни разходи, или чрез комплексна оценка:

При прилагане на подхода транспортни разходи се отразяват: доставката на суровините; пласмента на готовата продукция; осигуряването на работна ръка; състоянието на транспортната инфраструктура

Подход комплексна оценка (за общи разходи и/или въздействие) включва 5 етапа

1. Избират се подходящи критерии, които максимално покриват локализационните фактори и за които може да се набави информация.

2. Пресмятат се отклонения на значенията – минимални от максимални стойности, от средната стойност на показателя

3. Определя се точката еталон А0.Използват се стандартизираните отклонения -Това е точката с най-добрите стойности за отделните показатели

4. Изчислява се общото отклонение на всеки вариант за локализация от точката еталон.

5. Пресмята се обобщаващ показател. Отделните варианти се сравняват по отношение на големината на обобщаващия показател. Стойността е от нула до единица. Варианта, който получи стойност най-близка до 1.0 предлага най-добри условия за локализация.

Може да се даде и експертна оценка, която:

А. Да даде тежест на отделните критерии чрез теглови коефициенти

Б. Да отчете и допълнителни обстоятелства по локализацията

В. За факторите, които не са измерими количествено

Например, ако се изберат критерии материалоемкост, енергоемкост, трудоемкост и др., да се оценят като висока, средна или ниска за съответното производство. При отрасли с висока материалоемкост – се дава по-голям тежестен коефициент на материалоемкостта, при отрасли с висока трудоемкост – се дава по-голяма тежест на трудоемкостта.

Допълнителни обстоятелства към момента на избор, които могат да дадат основание за локализационно решение са показатели като:

-       Висока безработица

-        Възможности за разширяване

-        Възможности за съвместно ползване на складови бази, ремонтни бази, транспорт (локализационни икономии)

-        Дялово участие на общината

-        Спестяване на данъци

-        Отношение на местното население

-        ОВОС

-       Безопасност на обекта

6.2. Характеристики на моделите за общото равновесие

Моделите описани по-горе обясняват локализационния избор на отделната фирма и отделното домакинство. Това е познато в икономиката като частично равновесие. Освен това, предвид невъзможността да определят действителната стойност на земята (за да се определи общото локализационното равновесие), те приемат кривата на поземлената рента като израз на реалните пазарни разходи за земя.

Подходът „общо равновесие” е разработен в средата на 80-те години на 20-ти век като „нова урбанистична икономика”, или „икономика на моноцентричния град”. Този подход дава възможност да отстраним недостатъците на предходните модели. Моделите на общото равновесие, всъщност се стремят към определяне на пазарната поземлена стойност от условията за локализационното равновесие. Те са разработени с цел да се определи градската плътност, размера на града, както и стойността на земята за формиране на локализационно равновесие, при което всички домакинства са еднакво удовлетворени (или всички фирми имат еднакви печалби), запазвайки логическо-концептуалната рамка на модела на частичното равновесие. Има много изследвания по въпроса как да се определи не локализацията на отделното домакинство или фирма, в рамките на модела на частично равновесие, а да се определи локализационното равновесие характеризиращо се с еднаква полезност за всички домакинства или равна печалба за всички фирми, и да се определи гъстотата на населението на всеки град при тези условия.

При фирмите, предполагайки че:

• стойността на земята в края на града се равнява на стойността на земеделската рента и
• са известни:
• равновесното количество на стоката (т.е. количеството, което едновременно удовлетворява търсенето и предлагането на стоката),
• цените на други производствени фактори (освен земята),
• равнището на печалбата, желана от фирмите,

то моделите определят максималния размер на града, плътността на фирми, както и тенденцията на стойността на земята в зависимост от пространственото разположение (действителната крива на рентата). Същите характеристики (максимален размер, плътност, и цена на земята в пространството) се идентифицират от моделите отнасящи се за домакинствата, след като населението поиска да се насели в града – цените на другите стоки, както и желаната от домакинството полезност са зададени екзогенно. Този опит е пренесен в различни хипотези – съществуването на „затворени градове”, т.е. град, чийто демографски размер е определен от гледна точка на домакинствата (или пазарно равновесие при фирмите), и „отворен град”, в случая, когато размерите на града е ендогенно определен. Въпреки че моделите, които обсъждаме, са икономически логични, те често са изключително сложни. Затова представянето е опростено, доколкото е възможно.

Общ модел за равновесие при фирмите

Целта на модела на общото равновесие е да се определи – при даден процент (s) на градската земя използвана за производствени дейности – равновесната плътност на n фирми, намиращи се в градски район, всички специализирани в производството на една и съща стока (и се характеризират с една и съща производствена функция). Моделът предполага Коб-Дъглас производствена функция, състояща се само от два производствени фактори (земя и капитал), които могат да се заменят един с друг, и с постоянна възвръщаемост от мащаба:

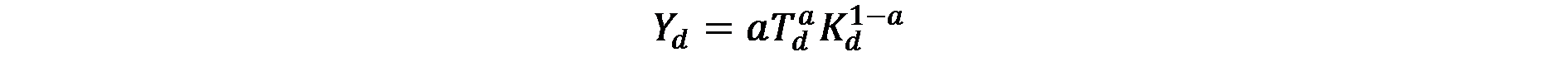 (6.1)

където Y е количеството на произведените стоки, a е константа, представляваща техническия прогрес, Т и К са съответно количеството земя и капитал, използвани в производствения процес, а и (1-а) съответно обозначават ефективността на производствените фактори „земя” и „капитал”.

Различните комбинации от производствени фактори за постигането на определено равнище на производство (Y) са представени на фигура 6.1-a от изоквантните криви. По-високи нива на производство се представят с отдалечаването на кривите от началото на координатната система. Когато те се съпоставят с изокостната линия, която представлява комбинациите от фактори с едни и същи производствени разходи, се определя комбинацията земя/капитал, която максимизира печалбата на фирмата (или при едни и същи приходи, разходите се намаляват), при дадено разстояние (d₀) от центъра (точка Е на фигура 6.1-a).

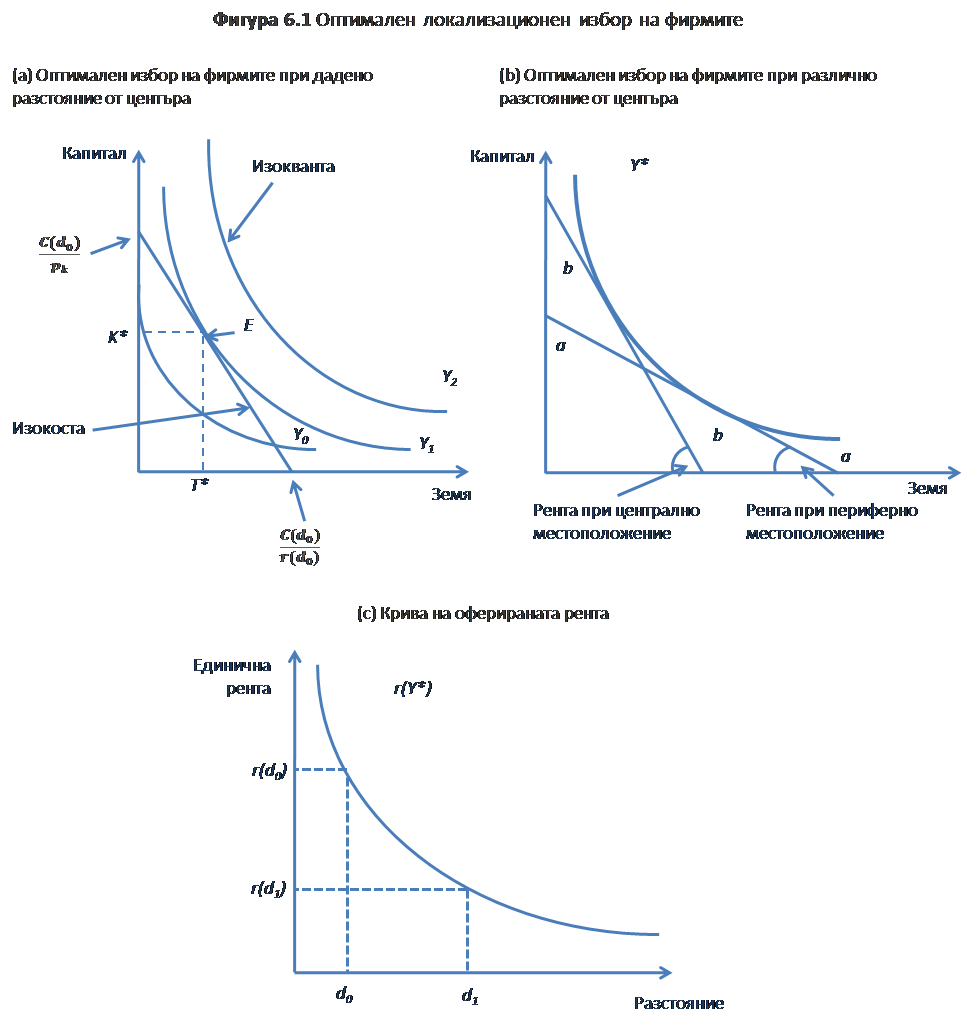
Ако фирмата иска да увеличи размера на градските земи, които използва, но да произвежда същото количество със същите разходи, тя ще трябва да намали размера на капитала, инвестиран в производствения процес. Фирмата ще има стимул да изберете точно такъв вариант, когато земята е по-атрактивна за нея, т.е., когато стойността на земята е по-ниска (фигура 6.1-b). По този начин, както се получи при модела с домакинствата, различните наклони на изокостната линия за различните разстояния от центъра, напр. рk, идентифицирайки кривата на рентата (фигура 6.1-c) – при дадено равнище на печалба (т.е. по една дадена изоквантна крива). С намаляване на разстоянието от центъра, бюджетна линия става по-стръмна, защото максималната оферирана рента за това разстояние нараства, както е показано. Кривата на поземлената рента се определя като:

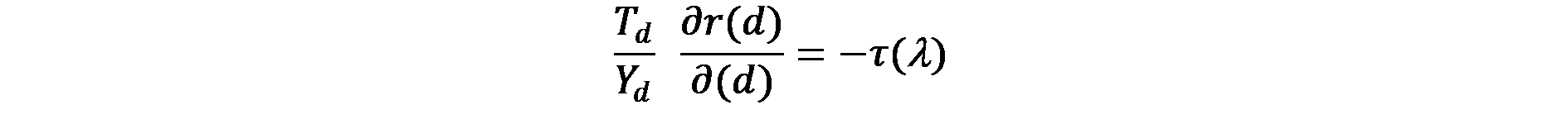 (6.2)

Това уравнение е условието на Muth при случая за фирмите. То посочва, че фирмата е безразлична към локализацията, когато новото локализационно предимство свързано със спестяване на транспортни разходи е равно на увеличение цената на градските земи. За да се компенсира увеличаването на разходите за земята, фирмата ще предпочете да използва по-малко количество земя, която е станала относително по-скъпа, като я замени с допълнителни количества капитал, например чрез изграждане на по-високи сгради. По този начин ще използва по-малко земя за единица продукция (Td/Yd ще бъде по-ниско).

Можем по този начин още веднъж да кажем, че всяка фирма е безразлична към алтернативните локализации по протежение на кривата на оферирания наем. С други думи, разходите за преместването в пространството са нула, така че всяка алтернативна локализация прави печалбата на фирмата непроменена.

Преминавайки към общото равновесие, при положение, че n фирми имат една и съща производствена функция, и че равновесното количество на стоката в града (Y*) е известно, то става възможно да се използва „гранична крива на рентата” за определяне на интензивността на използване на земята, максималното ниво на печалба постижимо от всяка фирма и общия размер на града. Граничната крива на наема определя всяко максимално ниво на печалба на фирмите (и от там за всяка крива на оферирана рента), при който произведеното количество е в равновесие.

Ако приемем, че стойността на земята в края на града е известна и равна на стойността на земеделската земя, може да се определи равновесната крива на рентата. Това е тази крива на рентата, която пресича граничната крива на рентата за земята в покрайнините на града (brc на фигура 6.2-a).

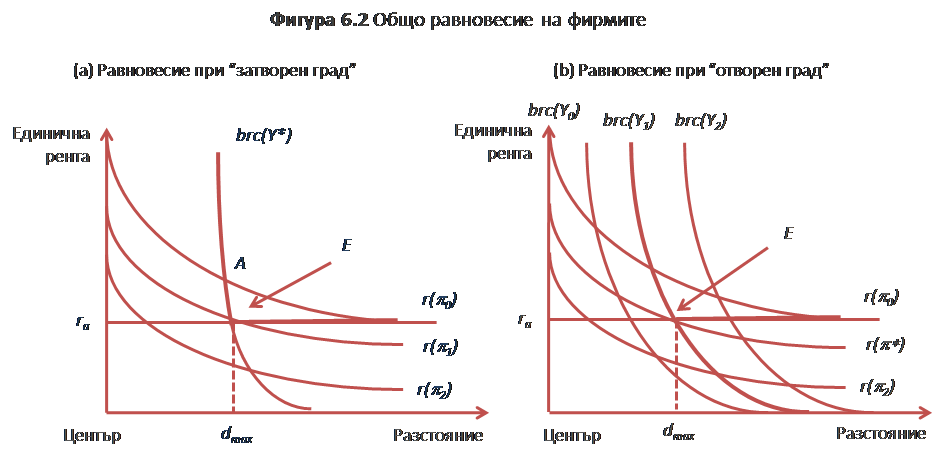
Причините за това твърдение са следните:

- По-високите криви на оферираната рента логично са изключени от определението за равновесно състояние, тъй като те определят равнищата на индивидуалните печалби, които са по-ниски от тази, която фирмите могат да постигнат (Фигура 6.2-a, всъщност точка E е определена за по-високо ниво на печалбата от А).

- По-ниските криви на оферираната рента са също логически неприемливи за дефиниране на равновесието, тъй като те определят стойността на земята в крайните градски райони, която е по-ниска от земеделската рента. Единствената приемлива рента гарантираща равновесие е тази, която пресича граничната крива на рентата на равнището на земеделската рента.

Точка Е на фигура 6.2-a определя:

• кривата на пазарната поземлена рента, предварително дефинирана екзогенно и съвпадаща с кривата на оферираната рента, за градове с размери по-малки от d_max, и с r_a за градове с по-големи размери;

• индивидуалното ниво печалба (π₁), постигнати от фирмите в града;

• максималния размер, достигнат от града (d_max).

Този модел показва също, фирмите разположени в градските райони съгласно равновесната плътност, която се получава след като максималният размер е определен. Безразличието към алтернативни локализации е характерно за всяко разстояние от центъра, тъй като по-ниският наем за предградните места точно компенсира по-високите транспортни разходи и дава възможност за икономии на капиталови разходи (намаляване на размера на земята, използвана за единица продукция).

Интересен случай е този, при който се приема т.нар. „открит град”, където фирмите могат да се преместят в други градски райони. Има няколко гранични криви на рентата в този случай, всяка от тях изразява равновесното ниво на производството на стоковия пазара (фигура 6.2-b). Локализационното равновесие се получава чрез екзогенно определяне на нивото на печалбата, външно и вътрешно в града равен на π*. Точката, в която кривата на оферираната рента гарантираща печалба π* пресича земеделската рента определя размера на града (и неговата плътност). Пресечната точка на кривата на оферираната рента с една от граничните криви граница на рентата показва действително произведеното равновесно количество (brc (Y₁) на фигура 6.2-b).

Модел на общо равновесие за домакинствата

Разсъждението е много подобно на това, приложено при модел на общото равновесие на фирмите. Определя се локализационното равновесие на n брой домакинства в един град. Общото равновесие на домакинствата първо изисква да има безразличие към други местоположения при всичките n домакинства, както е според условието на Muth. При хипотезата, че всички домакинства имат едни и същи доходи и същите структурни предпочитания, те проявяват безразличие по протежение на същата крива на рентата. Фигура 6.3-a показва различните криви на рентата.

Въпреки това, пазарната крива на поземлената рента вече не е известна, за разлика от модела за частично равновесие. Тя трябва да се определи чрез сравняване на кривите на оферираната рента от страна на различните домакинства, както се определя пазарната крива на поземлената рента при модела на Von Thünen, чрез описаната крива от поземлената рента на тримата фермери.

Както и случая с фирмите, възможно е да се използва гранична рентна крива за определяне на пазарната крива на поземлената рента (полезността за домакинствата). За всяко ниво полезност на домакинствата, а следователно и за всяка крива на оферираната рента, има максимален размер на града при всяко възможно разстояние от центъра.

Тази крива очертава градската зона при различни нива на полезност и различни максимални размери на града (при условие, че общото население е равно на екзогенно дефинираното) – ако полезността нараства, то и необходимото пространство за всяко домакинство расте, което води до намаляване на гъстотата на населението.

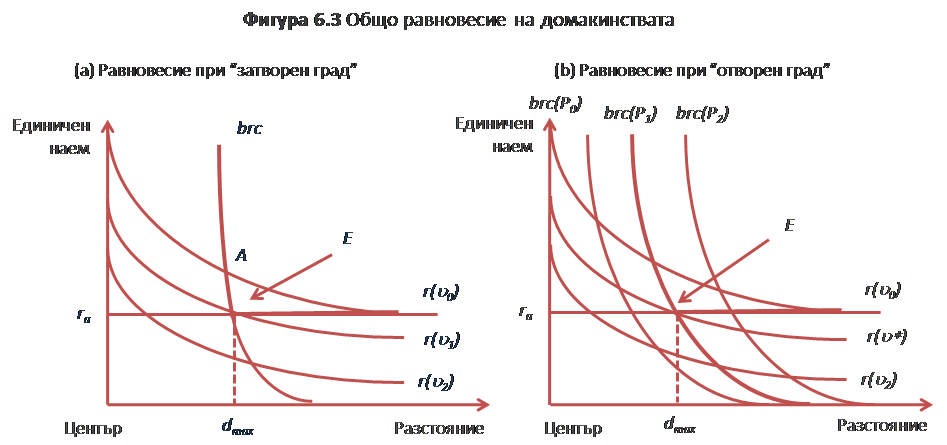
Както и в случая с фирмите, приемайки, че стойността на земята в крайградските зони е известна и равна на стойността на земеделски земи, е възможно да се идентифицира равновесната оферирана рента. Това ще бъде тази крива на оферираната рента, която пресича граничната крива на рентата за стойност на земята в крайградската зона (brc на фигура 6.3-a). Ако граничната крива на рентата се пресича с най-високата оферирана рента (точка А на фигура 6.3-a), домакинствата ще бъдат принудени да преминат към по-ниски криви на рентата, които изразяват по-голяма полезност.

Ако обаче пресичането е с по-ниска крива на оферираната рента няма да има равновесие, защото цената на земята предлагана от домакинствата за най-отдалечения край на града ще бъде по-ниска от стойността на земеделската земя.

Както и в случая на фирмите, точка Е на фигура 6.3-a определя:

•            пазарната крива на поземлената рента, предварително дефинирана екзогенно и съответстваща на кривата на офериранта рента, за град с размери по-малки от d_max, и с r_a при по-големи градове;

•            нивото на полезност (uj), постигнато от домакинствата в града;

•            максималния размер и плътност, постигнато от града (Jmax).

В случай на „отворен град” (където домакинствата могат да се преместят в други градове) там съществуват (както е в случая с модела на фирмите) няколко гранични криви за граница на рентата, като всяка съответства на различен брой на населението (Фигура 6.3-b). Равновесието се получава, като екзогенно се определи нивото на полезност външна и вътрешна за града, която се равнява на u*. Точката, в която кривата на оферираната рента гарантираща равнище на полезност u* пресича поземлената рента посочва размера на града (и неговата плътност). Пресечната точка на кривата на оферираната рента с една от граничните криви на наема показва населението в равновесие (brc(P₁) на фигура 6.3-b).

И накрая, нека отхвърлим хипотезата, че всички домакинства имат един и същи доход и приемем, че съществуват три класа с различни доходи и различна структура на предпочитанията. Наклонът на кривата на оферираната рента ще се различават в зависимост от равнището на доходи. С увеличаване на дохода, различните класове домакинства ще бъдат склонни да плащат повече за къщата, за да се локализират (една единица разстояние), по-близо до центъра (фигура 6.4). Трите класа домакинства са разпределени в населеното място както в модела на Thünen – всяка зона ще бъде заета от този клас домакинства, които предлагат най-висок наем. Пазарната поземлена рента ще бъде обща крива от кривите на оферираната рента за всяко разстояние до центъра, така че градът може да се опише като набор от концентрични пръстени всеки, от които съдържа класа на домакинствата, готови да платят най-високия наем за това разстояние (фигура 6.4).

Фигура 6.4 Локализационно равновесие при домакинствата

6.3. Фирмите и домакинствата – в равновесие

И накрая, има модели на моноцентричните градове, които, с малки корекции позволяват едновременно анализ на локализациите на фирмите и домакинствата. При хипотезата, че градиентът на наемът на фирмите е по-голям от този на домакинствата (т.е. фирмите са готови да плащат по-висока наем, за да се придвижат една единица разстояние по-близо до центъра), кривите на оферираните ренти при фирмите и домакинства ще бъдат тези, показани на фигура 6.5.

Фигура 6.5 Локализационно равновесие на фирмите и домакинствата

Тези модели водят до два важни резултата. Първият е, че те определят кривите на оферираните ренти при фирмите и домакинствата ендогенно. Нека приемем, че в момент t₀ домакинствата избират ниво на наема r₀ характеризиращ се с определено ниво на полезност. За да настъпи равновесие, нивото на полезност трябва да бъде такова, че да предпостави такъв брой население и предлагане на труд, което да е равно на търсенето на труд от страна на фирмите. Ако домакинствата са избрали твърде високо ниво на полезност, и затова се оферират наеми, които са твърде ниски, населението, което ще се настани в града (в диапазона d₁ – d^’_max) може да бъде недостатъчно, за да отговаря на търсенето на работна сила от страна на фирмите. Наличието на работа ще привлече нови домакинства в града, което води до увеличение на търсенето на градски земи, което изтласква кривата на оферирания наем до r, на фигура 6.5. Градът ще се разшири (d"_max), докато се възстанови равновесието на пазара на труда при по-ниско ниво на полезност.

Вторият важен резултат от тези модели е, че те разделят градската зона на производствени и битови дейности. Градските земи ще отидат при онези дейностите, които могат да плащат по-висок наем за всяко разстояние от центъра – както в модел на Thünen. В този случай, централната зона ще бъде заета от фирми, докато домакинствата ще бъдат изтласкани към крайните градски зони – теоретичен резултат, който добре отразява това, което се случва в действителност.

Като се започне от хипотези, подобни на тези на класическия модел на Thünen моделите, описани тук приемат неокласическата рамка (максимизация на печалбите на фирмите и максимизация полезността за домакинствата), при определяне условията за локализационно равновесие за производствените и битови дейности, пространствената схема на цените на урбанизираните земи, както гъстотата и големината на града.

Моделите очертават микроикономически концепции, за да обяснят чисто пространствени явления, като разпределението на дейностите в пространството и локализационния избор на домакинствата и фирмите. Така се отстраняват бариерите между основните икономически учения и урбанистичната икономика, които дълго възпрепятстват развитието на общата теория за пространството. Традиционната икономика се обогатява с теории, които обясняват пространството в чисто икономически смисъл, а урбанистичната икономика възприема традиционната икономическа логика, чрез която обяснява локализационния избор.

Освен това, въпреки че тези модели са много абстрактни (изотропно пространство, град с един център), те са в състояние да опишат условия, които са близки до реалните – наемът на урбанизираните земи има отрицателен наклон спрямо разстоянието до центъра (фигура 6.6), централното локализиране на дейности с висока добавена стойност (бизнес и управление), широкото крайградско пространство за битови дейности.

Все пак, въпреки тяхната логика и икономическа строгост, тези модели имат редица теоретични елементи, които отслабват цялостната им логическа структура. Един от тях е решаващата роля, която играе пътуването при определяне на локализационното равновесие. Ако реалното поведение не съответства на перфектната рационалност, предвидена от моделите, то пътуването ще е с по-малко значение за полезността при отделните лица и цялата теоретико-концептуална рамка се нарушава. Въпреки това, този недостатък може да бъде частично отстранен, ако признаем, че разходите за транспорт до центъра и желанието да ги намалим могат да отразяват и други важни аспекти на функцията на полезността при отделния индивид, когато той/тя прави локализационен избор, например достъпността до информация, развлекателни услуги, възможностите за социално общуване.

Вторият недостатък е по-сериозен. Тези модели не се занимават нито с това как е организиран градския център, нито с това, което се случва извън самия град. Те се ограничават с обяснение на локализационното поведение в рамките на зона, простираща се между хипотетичен пространствен център и физическите граници на града. Освен това, когато тези модели се използват за да се обясни локализационното равновесие не вътрешно за един град, а между градовете (т.е приемайки хипотезата, че града е част от една урбанистична система и, че фирмите и домакинствата могат да решат да се преместят в други населени места с атрактивно по-високи нива на полезност или печалба), те демонстрират слабост при интерпретацията на резултатите. На базата на хипотезата, че домакинствата имат еднакви структурни предпочитания и фирмите имат еднакви производствени функции, може да има безразличие към алтернативна локализация в други градове, само ако всички те имат една и съща крива на оферираната рента и една и съща гранична крива на рентата – така всички имат един и същи размер. Ако това е така, ще има една урбанистична система, съставена от градове, които са всички с еднакъв размер, но това обстоятелство напълно противоречи на реалния свят. За да се справи с този дефект, концептуалната рамка трябва да бъде в състояние да приеме хипотезата, че локализационните предимства са различни според размера на града, и така рентата (паричният израз на предимствата, които домакинствата и фирмите получават от централното си местоположение) са различни при различните градове.

Само по този начин е възможно да се постигне локализационно равновесие между населени места с различни размери. Това също изисква приемането на идеята, че големите, средните и малките градове са структурно различни и изпълняват различни функции в цялата икономика, и следователно имат специфична производствена специализация – хипотеза, противоречаща на основните характеристики на тези модели.

6.4. Обща достъпност и гравитационен модел

Тук локализацията на дейностите в градското пространство е обяснена от гледна точка на достъпността до общ централен бизнес район – мястото за търговия, информация, социални и икономически взаимоотношения. Центърът привлича фирми и домакинства, които на свой ред, въздействат на центъра по различни начини – ежедневни пътувания, разпространение на знания и информация, мрежи за сътрудничество и лични взаимоотношения. Тези сили на привличане (и отблъскване) засягат не само центъра, но всяка двойка точки в пространството (две различни зони на един и същ град, както и две различни населени места) и те се генерират от интензитета на потоците от хора, информация и стоки между тези точки. В действителност, тези потоци измерват отношенията, които могат да възникнат между дейностите, разположен в двете точки от пространството, а в един агрегиран мащаб, по-голямата привлекателност на една зона по отношение на другите (един град по отношение на други градове).

Изненадващо, потоците от хора, стоки и информация през една територия, изглежда че се организират въз основа на гравитационните полета чувствителни към размера на дейности, извършвани на територията, както и към тяхното относително отстояние.

От времето на George Kingsley Zipf в годините след Втората световна война, териториалните потоци от информация, стоки и хора са определяни като се използва гравитационния модел, наречен така, защото се основава на закона на Нютон за всеобщата гравитация. Според този модел всяка точка в пространството претърпява (или оказва) влияние пропорционално на масата и обратно пропорционално на разстоянието, което я отделя от останалите точки в пространството.

Моделът на потока (наречен така, заради способността му да оцени потоците между две териториални единици) се представя така:

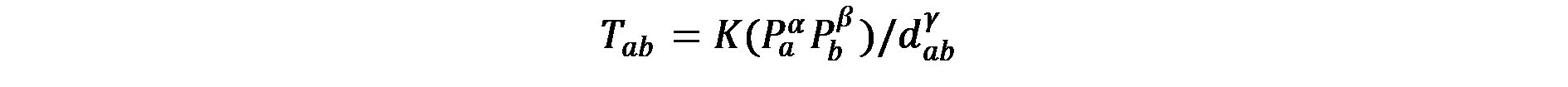 (6.3)

където Т е интензивността на взаимодействието между двойка a и b като точки в пространството, К е константа на пропорционалност, Р е масата на точки a и b, d е разстоянието между a и b, α и β се приемат за равни на 1. Експонентата на разстоянието γ, представлява съпротивление или триене, упражнявано от физическото пространство върху движението (на стоки или хора). Стойността му е различна според изследваното явления (например, по-голяма тежест има изминатото разстояние от дома до магазин, когато се купуват стоки от първа необходимост спрямо това при купуване на луксозни стоки като бижута). Масата Р на териториалните единици често се изразява с броя на населението.

Когато гравитационният модел се обобщи, така че да може да се прилага за оценка на потоците между една точка и n точки в пространството (например между една зона на града и всички други зони на града), отново се прави аналогия с гравитационната физика при тълкуване на териториалните явления чрез гравитационния модел представен по следния начин (известен като модел на потенциала поради измерване на потенциалната атрактивност на съответното място):

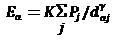 (6.4)

където E представлява потенциална енергия упражнена върху a от набор от маси Pj всяка на разстояние d от a. Параметър γ отново обозначава пространственото триене, което може да се различава от стойност единица, приета в оригиналния модел на гравитационната физика, като по този начин позволява прилагането на модела към териториален феномен с допълнителна степен на свобода.

От икономическа гледна точка, уравнението представлява „обобщена достъпност или взаимодействие”. Този показател измерва достъпността (или привлекателността) на всяка точка по отношение на пространството, което я заобикаля. Голяма информация се съдържа в общата достъпност на хипотетична зона i. Тя изразява: „демографски потенциал”, когато оценява ежедневните пътникопотоци от всички други зони на града, в зона i; „пазарен потенциал”, когато тя оценява потока от хора (потенциални клиенти) от всички други зони, към зона a, ако това е зона за търговия; „потенциал за доходи”, когато доходите на глава от населението е свързано с индивидите (потенциалните клиенти); „локализационен потенциал”, когато се използва, за да се обясни локализационния избора (направен за мястото с най-голям локализационен потенциал) и наборът от потоци не от това място (търсене на мобилност и транспорт). Локализационния потенциал обяснява и стойността, свързана с конкретно местоположение (наемът от предишните модели) от гледна точка на неговата атрактивност и общи достъпност.

Представените по-горе уравнения може лесно да се изчислят с прости иконометрични модели, след преобразуването им в логаритмична форма и последваща линеаризация на уравненията. Познаването на физическото разстояние между два града (или между две места в града), населението на двете места и потоците между две места, Т – на едно място с j други места, E, то статистически е възможно да се получат стойности на К,α,β и γ.

В оперативно отношение, тези модели имат капацитет да предвиждат, ако се използват за оценка на потенциалното въздействие на локализацията на нова производствена дейност в определен район. Например при проект за изграждане на търговски център в един район, когато стойностите на К,α,β и γ са изчислени и са известни:

• разстоянието между две точки в пространството,
• очакваното увеличаване на населението в района (напр. нови работни места),

то с първото уравнение може да определи броя на хората, които ще се движат от една зона а на града до зона i, а с второто уравнение, чрез модела на потенциала може да се прогнозира търсенето на транспорт, пазарния потенциал (потенциалният брой на клиентите на търговски център), както и потенциалните приходи, свързани с изграждането на търговски център.

В този раздел бяха описани модели, от чисто неокласически характер, чиято цел е да се отчете разпределението на земята между алтернативни дейности в рамките на пространствената структура на еднородно предлагане в пространството и точков източник на търсене. Търсенето на достъп до централни райони води до конкуренция между фирмите и домакинствата за получаване на места по-близки до пазара, или по-общо казано – до един хипотетичен централния бизнес район.

Стойността на земята е основният фактор, който организира дейностите в градското пространство. Съгласно строгата икономическа логика, конкуренцията за земя, близка до центъра намира своето решение чрез преминаването ù към дейности в състояние да плащат по-високи наеми.

Добрите страни на тези модели са строгата и последователна икономическа логика. Тяхната основна слабост се появява, когато те се опитват да обяснят локализационния избор, направен от домакинствата и фирмите при градове с различна степен на полезност или печалба.

Безразличието към алтернативни локализации, което е условие за дългосрочно равновесие, е гарантирано, само ако градовете предлагат една и съща полезност и печалба, и следователно, според логиката на модела, само ако градовете са с един и същи размер. Но това означава, наличието на урбанистична система, състояща се от градовете, които са с еднакъв размер – едно обстоятелство опровергано от реалността. За да се разберат икономически причини за съществуването на урбанистични системи с градове с различни размери, трябва да бъдат взети под внимание функционалните характеристики на градовете. Това е един аспект, с който моделите, описани до този момент не са в състояние да се справят, и който е съобразен в моделите, разгледани в следващата тема.