ТЕМА 07:

ЛОКАЛИЗАЦИЯ И ЙЕРАРХИЧНА СТРУКТУРА

 

Локализационните модели, разгледани в предходните раздели, анализират локализационния избор основно на отделните фирми (домакинства). Те се абстрахират от наличието на други дейности и е характерна дихотомност на локализационните алтернативи – градски и извънградски райони, централни или периферни такива, райони с високи или ниски концентрации на дейностите. Дори когато се приема съществуването на няколко дейности, не се анализира възможността тези дейности да могат да бъдат в алтернативни градски центрове. Така че, когато някои модели разглеждат съществуването на няколко дейности, те достигат до извод, който не съответства на действителността, а имено, че равновесните урбанистични системи са такива с еднакъв размер. Така се гарантира едно и също отношение на субекта на локализация към алтернативни локализации, защото нивото на печалбата и полезността са еднакви във всички градове.

7.1. Географски подход: модел на Walter Christaller

Има разработени теории, които могат да обяснят локализационен избор на няколко фирми и домакинства между алтернативни градските центрове. Така може да се обясни защо в действителност съществуват множество градове с различни размери и различни функции, т.е да се обясни защо съществува йерархия на градовете.

Тези теории се стремят да отчетат съществуването на градски системи състоящи се от градове с различни размери. Целта на тези теории е да се формулират правила, чрез които може да се интерпретира йерархията на градовете, като се обясни:

- размера и честотата на градските центрове на всички нива в йерархията, и следователно на пазарния ареал на всеки от тях;

- разстоянието между даден град, и градовете, намиращи се на нивата, непосредствено под или над него в йерархията, и така да се определи географското разпределение на всички градски центрове.

Основателите на тази школа, известна като „теория за централното място”, са географа Walter Christaller и икономиста August Lösch (снимка). Те първи формулират модели, способни да обяснят йерархията на градовете, и те подготвят почвата за последващи анализи.

Моделът на Christaller се основава на предположението, че един градски център съществува, когато има стоки и услуги, които да се търгуват. Това централно „място” (оттук и името на теорията „теория за централното място”, известен като модел на Christaller) трябва да произвежда или предлага стоки и услуги на населението, което е пространствено разположено в еднородна и изотропна обкръжаваща територия. Целта на моделът е да покаже как стоките и услугите започват да се организират териториално в една йерархия на градовете.

За тази цел Christaller въвежда понятията #праг на услугата# и #обхват на услугата#. Те изразяват от географска гледна точка икономическите сили, които организират дейностите в пространството – транспортни разходи и агломерационни икономии (вкл. икономии от мащаба). Обхватът на услугата е максималното разстояние, което потребителите са склонни да пропътуват, за да я закупят (което включва максимумът транспортни разходи, които те са готови да платят). Прагът на услугата е минималния пазар (население или доход), който очертава кръг (около центъра, който предлага услугата), с достатъчно население за генериране на такова ниво на търсене, че услугата да се продава. Услугата се произвежда само, ако обхватът надхвърля този праг. С други думи, услугата се произвежда само, ако има достатъчно търсене, за да бъде предлагана с реализиране на печалба.

Централното място се намира в центъра на пазар с кръгла форма, който е най-оптималното място, защото потребителите, намиращи се в района са в състояние да сведат до минимум своите транспортни разходи.

При равновесие, пазарните зони, определени от обхвата на стоката/услугата приемат формата на шестоъгълник. Тази геометрична форма дава възможност на Christaller да поддържа три основни предположения: (а) минимизиране на транспортните разходи за потребителите (шестоъгълникът е фигура най-близка по геометрична форма на кръг), (б) равномерно разпределение на предлаганата услуга, така че цялата територия се покрива, без областите, които са оставени необслужени; (в) конкуренция между производителите – пазарните ареали не се припокриват. При равновесие, се появява в пространството решетка на „пчелна пита”, състояща се от n центрове доставящи блага на n шестоъгълни пазарни зони, с един и същи размер (фигура 7.1).

Фигура 7.1 Организация на пазарните зони според трите принципа на Christaller

Според Christaller, всяка услуга има обхват, който определя размера на нейната пазарна зона – висококачествени стоки/услуги, произведени и предлагани в големите градски центрове, имат по-широк обхват, т.е очертават се пазарни зони по-широки от тези, в които се предлагат по-ниско качествени услуги.

След определянето на пазарни зони с формата на шестоъгълник, където стоката/услуга от реда n се предлага, Christaller определя пазарните зони от непосредствено по-ниския порядък. За тази цел, той допуска, че икономически единици от непосредствено по-ниския ред услуга ще избере локализация в централно място, където по-висок ред услуги вече се произвеждат – центровете на шестоъгълниците – така че могат да се реализират икономии от агломерацията.

Поради това, че по дефиниция обхватът на услугите от по-нисък ред е по-малък от този на услугите от по-висок ред, пазарната зона, обслужвана от икономически единици, разположени в центъра на шестоъгълника е по-малка, отколкото самия шестоъгълник. Следователно, част от територията остава непокрита. Това незадоволено търсене привлича в района нови единици за производство на услугата. Те избират своята локализация в съответствие с три различни принципа, които Christaller предвижда когато очертава пазарните зони в пространството:

1. пазарен принцип, който определя локализацията на еднакво разстояние от една тройка центрове от по-висок ред, представлявана от връх, образуван от шестоъгълниците с по-големия размер (фигура 7.1-а). Оптималността на тази локализация изпълнява критерия за свеждане до минимум броя на центрове, които покриват територията на пазара от по-висок ред. Според този локализационен модел, има 1 + 6/3 = 3 центъра от по-нисък ред в рамките на пазара от по-висок ред;

2. транспортен принцип, който важи за локализация на еднакво разстояние от една двойка центрове от по-висок ред (фигура 7.1-b). Този избор оптимизира местоположението на центрове от по-нисък ред на базата на минимизиране на транспортните разходи до центрове от по-висок ред. Във всеки пазар от по-висок ред има 1 + 6/2 = 4 центъра от по-нисък ред;

3. административен принцип, локализация в центъра на триъгълниците, съставляващи шестоъгълника (фигура 7.1-c), така че целта за оптималност е да се предотврати центрове от по-висок ред да се конкурират за администриране центрове от по-нисък ред. Тази цел се постига, ако центровете от по-нисък ред спадат към един център от по-висок ред. В този модел, има 1 +6 = 7 центрове от по-нисък ред за всяка пазарна зона от определен ред.

Така моделът създава йерархия на градските центрове – за всеки център (или пазарен ареал) от ред n има к центрове (пазарни зони) от ред n – 1; к е коефициент на съотношение между центъра от определен ред и този, който е под него, и стойностите му са 3, 4 или 7 в съответствие с прилагания локализационен принцип (пазарен, транспортен или административен). В модела на Christaller, този фактор (коефициент) е постоянен. За всеки к, може да се приложат прости правила, за да се получи броя на центрове от всеки ред, разстоянието между центровете от всеки ред, както и размерът на пазара.

Моделът достига до важен извод – всеки голям център произвежда стоки/услуги обвързани със своето йерархично ниво и с всички по-ниски редове (стоки и услуги). Големите предимства на центъра идват от функционалното ниво, характерно за йерархичния ред. Следователно, размерът на града определя функциите на града и всеки център има низходящ масив от центрове от по-нисък ред докато се достигне най-ниското ниво на агломерация.

Моделът на Christaller създава система от йерархични пространствени отношения, които са свързани със заобикалящата пазара среда. Въпреки че моделът е основно географски по характер, той прилага икономически постулати, като се основава на тях:

• Рационално поведение на потребителите, които намаляват транспортните разходи, така че да могат да закупят предлаганата услуга. Пазарните зони са отделни едни от други и не се припокриват;
• Хомогенно географско пространство, в което агломерацията на дейностите се случва по икономически, а не по физико-географски причини;
• Транспортните разходи са пропорционални на изминатото разстояние;
• Наличието на икономии от мащаба, като тези, заложен в концепцията за прага;
• В предлагането на услугата е заложено приемането, че територията трябва да бъде покрита, така че всички потребители да имат достъп до всички стоки и услуги.

Когато Christaller прилага модела си към действителността, той получава изненадващи резултати. Той първо анализа урбанистичната структура на Южна Германия, определяйки шест нива на центрове на основата на един избран индикатор – броят телефонни постове, свързани с междуградската мрежа. Когато след това се прилага пазарния принцип, той открил поразителна връзка между броя на центровете, определени от модела му и броя на реално съществуващите:

Необходимо е да се подчертае, че моделът на Christaller е в състояние да отговори на поставените въпроси: той показва наличието на йерархия на градовете, в която всеки град с определен размер, изпълнява специфична функция. Освен това, моделът е в състояние да осигури правила, с които да се определи броя на центровете от определен ред, размерът на всяка пазарна зона на всеки център, разстоянията между центровете от същия ред, и от там географското им разпределение.

7.2.Математическо представяне на модела

Моделът на Christaller е качествен в своята оригинална формулировка, но също е разработена и съвременна количествена версия. Нека с p₁ да бъде означено населението на населено място от по-нисък ред и с r населението на селски райони зависим от p₁. Населението на целия района, обслужван от p₁, обозначаваме с P₁ и можем лесно да го определим:

 (7.1)

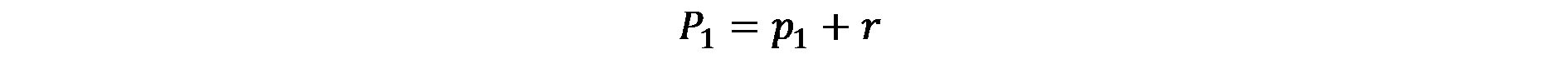
При хипотезата, че всеки град има население, което е постоянна част c на района, т.е.

 (7.2)

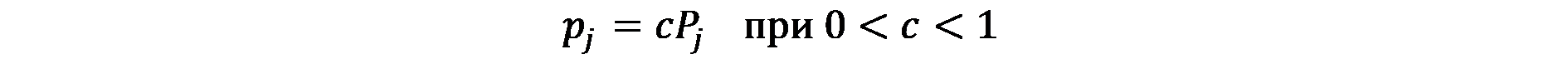
Уравнението може да бъде презаписано така:

 (7.3)

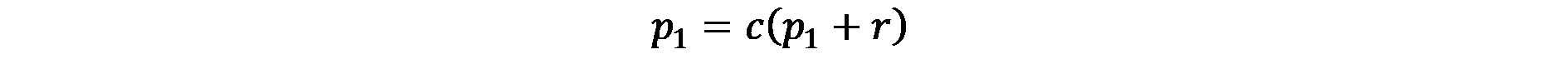
така че

 (7.4)

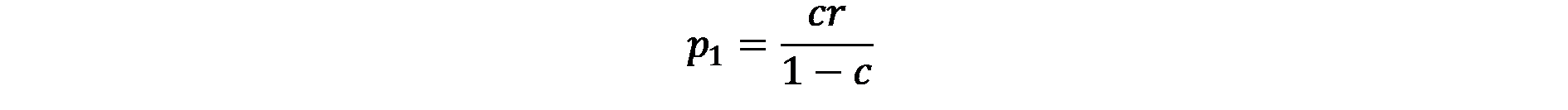
Последният вариант на уравнението показва, че населението на града, на 1-ви ред е равно на с/(1-с) умножено по населението на селския райони. В литературата с/(1-с) се нарича „мултипликатор на града”.

Нека приемем, че има n нива градски центрове и че всеки център обслужва себе си и s „сателитни” центрове около него. Населението на даден регион (P_n), обслужван от град от по-висок ред, се получава от населението на района от по-нисък ред (1 + s), имайки предвид, че център п поддържа население от ред n, а не от (n-1), в рамките на своя район:

 (7.5)

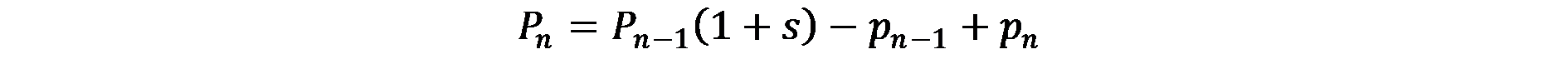
Като се има предвид (7.2), уравнение (7.5) може да бъде презаписано така:

 (7.6)

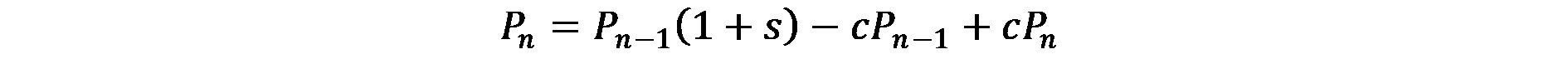
така че

 (7.7)

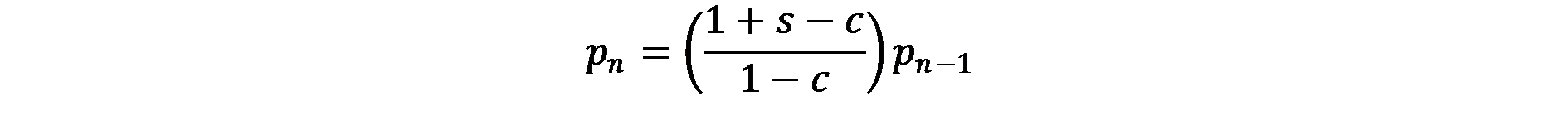
Тъй като в модела на Christaller s и c са константи в рамките на йерархията на градовете, последното уравнение определя постоянната връзка между размера на населението на региона и това на региона от по-нисък ред. Това уравнение може да се запише в следната обща форма:

(7.8)

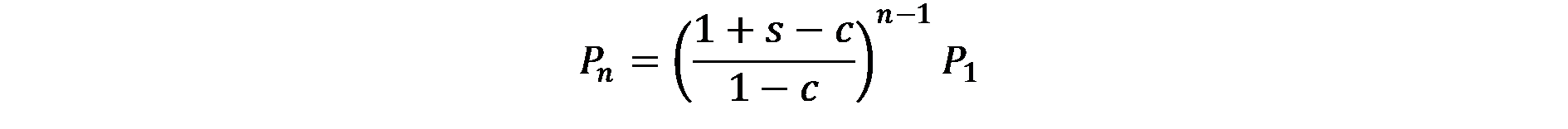
Ако заменим Р₁, с (7.4), когато умножаваме десния член с (1 + s — c)/ (\ + s — c), получаваме:

 (7.9)

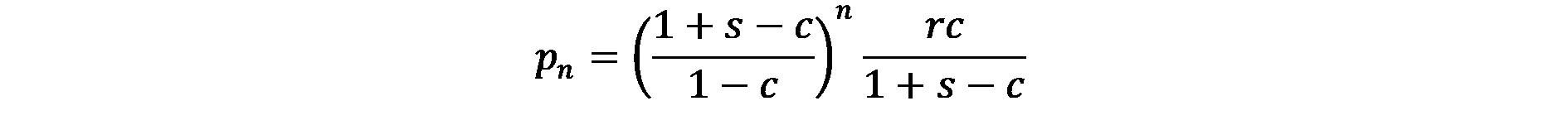
Уравнение (7.9) посочва, че знаейки населението на селските райони r, ние сме в състояние да намерим размера на пазарния ареал и население на центровете, от който и ред да е.

7.3. Икономически подход: модел на August Lösch

През 1940 г. August Lösch разработва модел на общото равновесие, за да отстрани основния недостатък на модела на Christaller, приемането, че коефициентът за пропорционалност е постоянна за йерархията на градовете.

Моделът на Lösch също разработва шестоъгълна структура на пазарните зони, но това става на базата на чисто икономически принципи:

• конкуренция между фирмите – това не позволява наличието на непокрити пазарни зони, тъй като потенциалните печалби в неконтролирани пространствени пазари привличат нови фирми в тези зони;

• рационалност на потребителите – когато потребителите трябва да избират между два възможни доставчика, тяхната рационалност ги предизвиква да изберат този, който предлага стоката на най-ниската цена, и следователно, според логиката на модела, те избират производител, разположен най-близо до тях.

Моделът на Lösch определя пазарните зони по експлицитните (макар и екзогенно) разходи и кривите на търсене на стоките, като по този начин постига пространствено равновесие на един отделен сектор. Моделът определя стабилно пространствено икономическото равновесие в шестоъгълните пазарни зони, което се достига, когато фирми вече нямат стимул да навлизат в пазара.

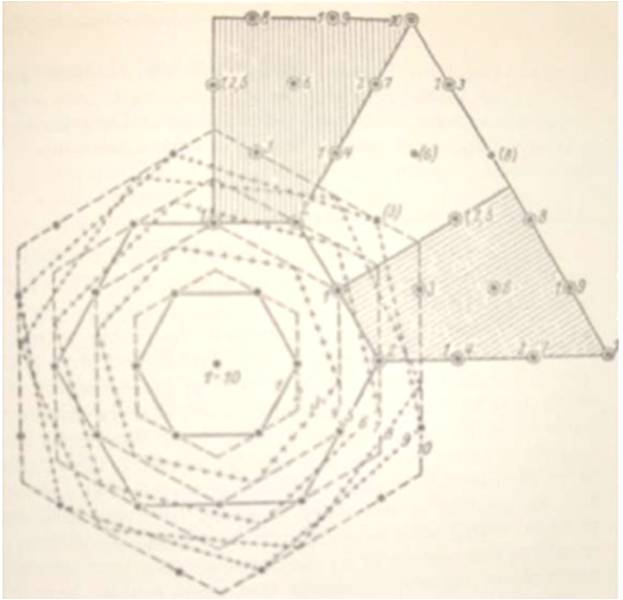
За разлика от Christaller, Lösch посочва няколко фактора (коефициента) на пропорционалност, наречени коефициенти на гнездене, които определят йерархията на градовете: к на Christaller е = 3, 4 и 7. Коефициентите днес приемат и други стойности на пропорционалност – 9, 12, 13, 16, 19, 21 (Фигура 7.2).

 

Lösch приема, че има специфична стойност на коефициента на гнездене, и затова специфични размери на шестоъгълните пазарни зони на пазара, съответстващи на всеки вид стока или услуга. Коефициентите на Lösch са просто кратни на коефициентите на Christaller (3, 4 и 7), и са съобразени с трите принципа на Christaller:

• 9 и 21 – с пазарния принцип: 9 = 1 + 6 + 6/3, и 21 = 1 + 6 + 6 + 6 + 6/3;
• 16 – с транспортния принципа: 16 = 1 + 6 + 6 + 6/2;
• 13 и 19 – с административен принцип: 13 = 1 + 6 + 6 и 19 = 1 + 6 + 6 + 6;
• 12 – с пазарен принцип и след това с транспортен принципа: 12=1+6+6/3+6/2

Приемането на константност на фактора (коефициента) за пропорционалност в рамките на урбанистичната йерархия води до някои последици. Елиминира се двупосочна връзка между размера на центъра и специализацията, и това дава възможност да бъдат разгледани такива важни емпирични ситуации като различната функционална специализация на центровете с един и същи размер, както и възможността центровете да имат функционални специализации – по този начин центърът може да изпълнява само функцията от своя ред, а не от всички други редове, което налага модела на Christaller.

Начинът, по който Lösch постига цялостно структуриране на територията, на основата на своите хипотези е интересен, но с някои недостатъци – организацията на икономическото пространство е резултат от наслагване на няколко шестоъгълника с различни размери и структури (съответстващи на различните видове стоки и услуги). Всички шестоъгълници имат общ център, който произвежда всички стоки (фигура 7.3а).

Фигура 7.3а

 

Окончателната структура на територията е получена чрез ротация на наслагваните шестоъгълници, за да се получи максимална плътност на центровете в някои райони, както и максимално съвпадение на различни производствени локализации (фигура 7.3-b – виж схема C). Резултатът е серии от кръгообразни алтернативни сектори с висока и ниска гъстота на населените места. Тези сектори се излъчват от един голям град като образуват структура, която е в съответствие с принципа за ефективността на транспортната система (фигура 7.3c).

Моделът на Lösch дава по-реалистични и по-малко парадоксални модели от тези, представени в модела на Christaller. Въпреки това, те се получават за сметка на размиването на концепцията за йерархия на градовете – липсват елементи в местата с висока плътност на градски центрове, които могат да се използват за идентифициране на йерархичната структура на центровете – поради липса, наред с останалите неща, на ясно разделение на труда при тях.

Lösch демонстрира валидността на модела си емпирично, като го прилага на територията на щата Айова в Съединените щати. Като допуска една градска структура, включващи шест нива в йерархията и гнездене с фактор 4, той получи следните резултати:

 

Както вече беше казано, за емпирична проверка на модела си Lösch предпочита да използва коефициент на гнездене 4, което съответства на коефициента за пропорционалност на Christaller при прилагане на транспортния принцип. Този принцип е съвместим с територията, избрана от Lösch за неговия емпиричен анализ, която е траверсирана от праволинейна транспортна инфраструктура.

7.4. Математическо представяне на модела

Подобно на модела на Christaller, Lösch също привлича интереса на редица икономисти, някои от които предлагат математическа формализация.

Официалният подход използва пет уравнения за състоянието на икономическите условия, които моделът разглежда като решаващи за постигането на общо пространствено икономическо равновесие. Последното произтича от два конкретни фактора: всеки производител се стреми да максимизира печалбата си, и всеки потребител се стреми да максимизира полезността си, чрез използване на най-евтиния пазар. Освен това, наличието на няколко фирми в същия сектор води до конкуренция между тях, което не допуска свръх печалби.

Условията са следните:

- Локализацията на производителите трябва да бъде възможно най-изгодна, така че никое придвижване в пространството да не води до повишаване на печалбата.

- Броят на възможните локализации да бъде такъв, че да се покрива цялата територия.

- Да няма свръх печалби, така че да се гарантира стабилност на пазара и да се възпрепятства навлизането на нови фирми.

- Обемът на произвежданата продукция и размерът на пазарния ареал да бъдат такива, че да съответстват на средните производствени разходи. Ако промяната в размера на пазара е свързана с увеличение на цените по-голямо от увеличението на средните производствени разходи, това ще генерира допълнителна печалба и ще се привлекат нови фирми на пазара.

- Продажната цена на стоката на границата между пазарните зони трябва да бъде една и съща, за да се гарантира на границата безразличие на потребителите към алтернативни локализации.

Тези икономически условия могат да бъдат превърнати в уравнения.

Като определим:

т = стоката, при което m = 1, 2, ... M;

п = център за производство на стоки, при което n = 1, 2, . . . N;

x_mn е у_тп = териториалните координати на всеки производствен център, има по 2 за всяко място n;

X_mn = количество от стока m, произведена в център n;

П_mn = общата печалба получена от продажбата на m в производствен център n;

c_m = средни производствени разходи за стока m;

p_m = продажна цена на стока m;

A = общ размер на територията, като A_m, A_m2, . . ., A_mn представляват размера на пазарните зони, където стока m е  продадена;

C_mn = границата на пазарната зона на производствен  център n за стока m;

d_mn = разстоянието между производствен център n и границата на неговата пазарна зона;

τ = единичните разходи за транспорт за стока m;

можем да презапишем петте условия със следните уравнения:

 

1.Условие от първи ред за максимизация на печалбата във всяка локализация:

       2N в брой (2 за всяка пазарна зона n)

2. Условие територията да бъде изцяло покрита от предлагането на всяка отделна стока

     M в брой

3. Условие за отсъствие на свръх печалба във всеки производствен център

     N в брой

4. Условие за минимален размер на пазарната зона, така че маржиналните промени в средните разходи да са равни на маржиналните промени в цената на стоката във всяко място, където се произвежда

     N в брой

5. Условие за равенство на цените на границата на всяка пазарна зона

     C в брой

Броят на уравнения, които трябва да се изчисляват в модела е 4N + М + С, което е равно на броя на неизвестните, като това са:

• размера на пазарните зони A_mn, които са равни по брой на центровете N;

• цените p_mn за всеки център, N на брой;

• броя на производствените центрове N_m, за всяка стока m, M на брой;

• координатите на всеки център x_mn и y_mn, 2N на брой;

• границите на пазарните зони, C.

Равенството между броя на неизвестните и броят на уравненията е необходимо условие за намирането на решение. Въпреки това, тъй като системата е нелинейна, може да има множество решения или липса на решение. Има различни начини за опростяване на системата от уравнения. Броят на неизвестните може да се намали чрез прилагане на правилна форма на пазарните зони, както е в оригиналния модел на Losch. В този случай, броят на границите на всяка зона става известен. Освен това, с N_m – 1 пазарни зони на стоката m, което е известно, на n-тата пазарна зона е разликата от общия размер на пазар А.

Във формализацията на модела на Lösch има някои слабости:

• Тъй като не е известен броя на центрове, в които се извършва производството, решението на модела е изключително сложно, поради това, че броят на уравнения, за да се отговори на първото условие е предварително неизвестен.

• В модела не е взето предвид евентуалното наличие на агломерационни икономии под формата както на урбанизационни икономии, типични за център от по-висок ред и така и локализационни икономии при по-специализираните центрове.

• Нелинейността на системата е такава, че не гарантира нито съществуването, нито уникалността, нито стабилността на равновесието решение

Моделът на Christaller и на Lösch се приемат за първите модели на общото пространствено равновесие. Ако предположим еднородност на пространство, то те са в състояние да обяснят (а) наличието на различни по големина градове; (б) ролята на всеки един от тях (в) разстоянието между тях. С една дума, тези модели за първи път правят възможно тълкуването на градските системи; едва напоследък се появяват предложения за нови модели за общото равновесие. Въпреки това, тяхната логическа структура не е в състояние да отчете наличието, при равновесни условия, на градски центрове с различен размер.

Така че и днес моделите на Christaller и Lösch са уникални инструменти, с които да се тълкува структурата на градските системи. Въз основа на съществуването на двете добре познати икономически сили определящи локализационния избор (агломерационните икономии и транспортните разходи), локализационното равновесие произтича от логиката за печалбата на фирмите и оптимизация на полезността за купувачите.

Въпреки това, двата модела имат редица слабости. Някои от тях произтичат от абстрактния характер на определени хипотези, например пространствената хомогенност на ресурсите и константност на единичните разходи за транспорт. Те не пречат на общото тълкуването, което дават моделите, пък и има потребност от опростяване на сложния характер на реалния свят. Моделите имат други недостатъци които са свързани с:

- Липсата на анализ на търсенето, като така се предполага, че то е равномерно разпределено в пространството. Също така, тези модели екзогенно определят количеството на всяка стока, търсена от потребителя. С други думи, това са подходи, които до голяма степен имат връзка с производствената теория.

- Липсата на взаимна връзка между производствения и локализационния избор на фирмите. Според модела, от гледна точка на предлагането, близостта до други фирми не влияе върху функцията на разходите; от гледна точка на търсенето не съществува взаимозависимост – на допълване и заменяемост, между стоките. Търсенето на една стока е независимо от цените на останалите стоки и независимо от локализацията на производителите на други стоки.

- Статичният характер на моделите. Това ограничава използването при анализ на развитието и динамиката в йерархията на градовете.

Първите два недостатъка са сериозни, защото те отразяват противоречията между резултатите и първоначалните хипотези, което пречи на интерпретативната логика на моделите. Наистина предположението, че търсенето е равномерно разпределено по територията си противоречи с основния резултат, че населението се концентрира в градските центрове. Концентрацията на производителите в определени точки в пространството в действителност изключва всякаква възможност за хомогенно търсене, тъй като тя предизвиква потребителите да се стичат до централно място предлагащо оптимални условия (стоки, които са евтини поради ниските транспортни разходи).

Моделите игнорират всяка локализационна взаимозависимост, както от гледна точка на предлагането, така и от гледна точка на търсенето. От гледна точка на предлагането, те не успяват да разгледат никаква връзка input/output, която може да благоприятства локализационния избор свързан с близостта на други доставчици. В резултат на това, тези модели нямат производствената функция, която свързва производството на една стока с друга. От гледна точка на търсенето, те не предлагат функция на полезността, която да прави връзка между стоките. Моделите не признават съществуването на заменяемост или допълване и така приемат формата на частично равновесие.

Christaller и по-специално Lösch, се позовават на концепцията за агломерационни икономии, за да обяснят локализационния избор на фирмите, но по-късно пренебрегват предимствата на тези икономии, като по този начин се накърнява „вътрешната съгласуваност” на моделите. Въпреки тези недостатъци, предвид тяхната уникалност и тяхната икономическа и географска концептуализация на градската йерархия, моделите на Christaller и Lösch все още заемат централно място в пространствената икономика.

7.5. Някои съвременни приложения

Christaller и Lösch са пионерите на това, което се нарича „теория за централно място”. Значителни усилия са направени за подобряване на оригиналните модели и да се коригират техните недостатъци и вътрешни противоречия.

Първото важно постижение на тези по-нови теории е създаването на модели с по-строг икономически характер и увеличаването на аналитичната сложност, което позволява да се включат аспекти на търсенето в общото равновесие. Моделът на Martin J. Beckmann и John C. McPherson постига успех. Този модел е в състояние да преодолее ограничението, наложено от постоянния гнездови коефициент (к в модела на Christaller, което Losch също се опитва да преодолее), както и постоянно съотношение между населението на центъра и населението на околността в рамките на градската йерархия (или в рамките на едно и също йерархично ниво на услуги, когато те са предоставени от центрове с различни размери). Моделът на Beckmann и McPherson допуска, че коефициентът на пропорционалност варира според йерархичното ниво на центровете и предлаганата услуга на равнище n. Значимостта на коефициента на пропорционалност вече не е географска, а икономическа (въпреки че се измерва от гледна точка на населението) и показва общия брой на лицата пребиваващи в центъра от ред a, необходими за предоставяне на съответната услуга на всеки жител от пазарната зона (включително самия център). С други думи, той представлява броя на хората, необходими за производството на стоки за цялата пазарна зона.

Hubert Beguin разширява модела на Beckmann and McPherson, за да включи два икономически аспекта, които оригиналният модел определя като детерминанти на съотношението между населението на центъра и населението от околността – производителността на труда (т.е. броят на хората, необходими, за да производство на единица от стоката m) и структурата на личното потребление (т.е. количеството на стока m, търсена от всеки жител на пазарната зона на центъра n). Beguin е в състояние да докаже, че в действителност структурата на градската йерархия – от гледна точка на съотношението между населението на центъра и на селския район около него – зависи от:

• вариране производителността на труда в различните нива от йерархията на центъра (нарастваща, намаляваща и постоянна възвръщаемост на труда);

• разпределението на различните видове стоки/услуги в общото търсене;

• доходната еластичност на търсенето при различните стоки.

Теорията за „централното място” прави поредна стъпка напред чрез въвеждане предимствата на локализационните икономии в моделите на Christaller и Losch. Забележителен принос в това отношение е направено от W. Long, който включва взаимозависимост между стоките в модел на Christaller. Той допуска, че количеството закупено от стока m не е задължително да намалява с увеличаване на разстоянието от центъра. Въпреки, че цената на стоката m нараства, когато човек се отдалечава от центъра, тя може да се намали, когато човек се обърне към други центрове, постигайки локализационни икономии произтичащи от близостта до тези центрове. Long посочва също, че обхватът на една стока може да се променя според това дали тя се произвежда в по-малък център или по-голям. За по-голям център, той отнася по-малък обхват, поради наличието на по-голям брой стоки-заместители на по-широкия градски пазар. Въвеждането на тези хипотези нарушава обичайния модел на Christaller и Lösch, и механизмите на взаимозависимост, по отношение на търсенето и предлагането, може да деформират резултатите, получени от оригиналните модели. Моделът на Long е един опит, чиято математическа сложност не позволява получаването на аналитични решения.

И накрая, теорията за „централното място” прави трета стъпка напред в отговор на необходимостта да се разбере не само градската структура, но и да се постигне нейното развитие и динамика. Тук основен принос има John Parr със сравнителния си статичен модел, който анализира развитието на организацията на територията на градската йерархия при следните хипотези:

• създаването на последователни нива на йерархията от най-ниското до най-високото;
• промяна в разпределението на икономическите функции на различните нива в йерархията;
• промени в йерархична структура, т.е. в броя на нивата свързани с различните по размер центрове: формиране на ново ниво в йерархията, промяна в разширяването на пазарната зона, изчезване на йерархично ниво.

Parr модифицира структурата на шестоъгълните пазарни зони, предложен в оригиналния модел на Christaller – те могат да се превърнат в правоъгълна или триъгълна или шестоъгълни зони с различни размери в рамките на градската йерархия.

7.6. Нова теория на градските системи

Градски мрежи

През последните години, градските системи на развитите страни са се развили по начин очевидно в противоречие с йерархичния модел на Christaller. Средните градове (40000 до 200000 жители) са претърпели забележително развитие и сега се характеризират с близка взаимозависимост с центровете от същия порядък, ясно изразена продуктова специализации и отсъствието на йерархични връзки в рамките на отделните градски системи. Развитието през последните двадесет години показва, че градските системи нямат нищо общо с йерархичната структура на Christaller. Те проявяват следните характеристики:

• градска специализация, особено в промишлеността, но и в сферата на услугите, което противоречи на прогнози на Christaller за йерархична деспециализация на всеки център;
• непълно присъствие на целия набор от функции във всеки град;
• функции от висок ранг в центрове от по-нисък ред;
• хоризонталните връзки между градовете, изпълняващи подобни функции: например #мрежа от градове#, специализирана в международните финансови услуги;
• взаимодействие между подобни центрове извършващи модерни функции за производство и услуги, както в примера с подрегионални промишлени райони. Тези емпирични резултати демонстрират неадекватността на традиционния модел на Christaller, който не обяснява очевидното явление за развитието на градските системи в развитите страни. Това води до разработване на нова концептуална парадигма за мрежите от градове, която представя по-убедително и ясно тълкуване на появяващите се териториални модели.

Тази нова парадигма предвижда възможността за поява на близки отношения между градските центрове, които си сътрудничат и взаимодействат на основа на конкретни икономически отношения. Тези отношения може да са вертикални между градовете от различен ред или (и това е много по-иновативен аспект) те може да са хоризонтални при градовете от същия порядък, които си взаимодействат на базата на взаимно допълване и синергия. В светлината на тези два процеса е възможно да се идентифицират два вида мрежи от градове: #допълващи се мрежи#, състоящи се от специализирани и допълващи се центрове, свързани от набор от input—output връзки. Секторната специализация гарантира икономии от мащаба и агломерационни икономии дори в центровете с малки размери. Примери за този вид мрежа от градове са специализираните градове на регион Рандстад (Холандия), или на полицентрична структура на градовете от региона Veneto в Италия. #Синергични мрежи# е другия вид мрежи, съставени от подобни и взаимно сътрудничещи си центрове; икономиите от мащаба се гарантират от сътрудничеството в самата мрежа, която свързва пазарите на отделните центрове. Примери за този вид мрежи са финансовите центрове, които функционират в целия свят, чиито пазари са практически свързани от съвременни телекомуникационни мрежи, или мрежи от градове свързани от религиозни туристически маршрути, създадени за честванията на юбилеите на Ватикана.

Трета категория мрежи, която може да бъде разглеждана като подкатегория на втората, са #иновационните мрежи#, състоящи се от центрове, които си сътрудничат по специфични инфраструктурни и производствени проекти, за да се достигне критичния обем по отношение на търсенето и предлагането. Примери за този вид мрежи е споразумението между френските градове за изграждане на инфраструктури.

Новата парадигма за тълкуване на градските системи има множество оригинални характеристики. Първо, понятието “мрежа от градове” излиза извън териториалния смисъл на йерархичните отношения между градовете, които притежават неприпокриващи се пазарни зони и в тясно сътрудничество един с друг. Фокусът вече е взаимоотношения между градове с един и същи размер, намиращи се на големи разстояния, които по дефиниция не могат да съществуват в модела на Christaller.

Освен това моделът, основан на „мрежови” отношения между градове отхвърля принципите за икономическа ефективност (намаляване на транспортните разходи и максимализиране на пазарната зона на центъра), които са в основата на организацията на градските центрове в йерархичния модели. Сега от първостепенна важност са новите принципи за икономическа ефективност, които определят организацията на градските системи и са свързани с положителните ефекти от съвместните или допълващи се дейности. В случая на синергичните мрежи, предимствата са наречени „мрежови външни ефекти”, които се отнасят за всички членове на мрежата. Пример за това са предимствата на международните финансови центрове от създаването на телематични мрежи и „виртуален” пазар, който им позволява да работят на големи разстояния и да имат относителни икономии от мащаба. В случая на комплементарните (допълващите) мрежи, предимствата са тези на териториалното разделение на труда и специализация, които се постигнат чрез увеличаване на хоризонталната интеграция между производствени единици и вертикалната интеграция в определени специализирани вериги.

Според парадигмата за мрежата от градове, следователно, взаимоотношенията между градските центрове вече не се ръководят от една ясна йерархия между центровете, или от конкуренцията между тях, при което локализационните икономии, както и input—output връзките засилват растежа на един център в ущърб на друг. Икономическите отношения между центровете са вече на базата на връзки за сътрудничество, които позволяват да се реализират икономии от мащаба, без да е необходимо градовете да растат по отношение на физическия си размер.

Така че можем да определим мрежата от градове като набор от хоризонтални (но не йерархични) взаимоотношения между допълващи се или подобни центрове. Тези отношения генерират икономии или външни ефекти като специализация/разделение на труда и синергия/сътрудничество/ иновативност.

Емпиричните изследвания напълно демонстрират тенденцията градските системи да се организират в мрежи, но те не отчитат размера на предимството, създадено от този тип организация. Едва наскоро има опити да се проверят положителните ефекти от съвместни или допълващи се дейности. Едно иконометрично изследване, приложено за „Healthy Cities Network” (институционална мрежа от градски центрове създадена с цел да подпомага и координира градските политики за защита на качеството на живот в градовете) на Световната здравна организация показва, че в мрежовата организация има положителни ефекти. Градовете най-тясно свързани с мрежата са били най-успешни по отношение на изпълнението на своите градски политики.

Макар че парадигмата „мрежа от градове” не може да се нарече теория, в някои отношения замества традиционния териториален подход на Christaller към изучаването на градските системи и тяхното развитие. Без съмнение, парадигмата представлява голям теоретичен напредък в йерархичния модел. Един добър пример за нейната тълкувателна сила е способността да прекрати механичната връзката между специализацията и размера на град, наложена от модела на Christaller. Това обяснява, например, защо Цюрих (град с 300 000 жители), осъществява функции от първостепенно значение за международните финанси, заедно с мегаполиси като Ню Йорк и Токио – обстоятелство невъзможно да си обясним чрез йерархичния модел на Christaller.

Чрез представените теории се обясняват икономическите причини за съществуването на градските системи, съставени от градове с различни размери и се преодоляват ограниченията на другите подходи, описани в предходните раздели. Централно място заемат теориите на Christaller и Lösch, които обясняват как градските системи се организират по територията според строгите икономически принципи. Обсъдената парадигма „мрежи от градове” е най-новата концептуализация на организацията на градските системи. Този подход вече не тълкува градските системи по отношение на чисто йерархичните отношения между градовете (които дават възможност за контрол върху неприпокриващи се пазарни зони и вградените една в друга). Вместо това, тази парадигма разглежда хоризонтални връзки между градските райони с еднакъв размер и между такива изпълняващи подобни функции. Тези отношения съществуват в реалния свят.