ТЕМА №11: „INPUT-OUTPUT” АНАЛИЗ. ЕКСПОРТНО-ОРИЕНТИРАН МОДЕЛ. НЕОКЛАСИЧЕСКИ МОДЕЛ НА ИКОНОМИЧЕСКИ РАСТЕЖ

Докато експортно-ориентираните модели на икономическия растеж са в състояние да измерват степента, в която местните продукт се променя с вариране на външното търсене, има метод известен като „input-output” анализ (входно-изходен анализ), който позволява да се направи оценка за въздействието на увеличеното търсене в определен сектор върху производство на всеки отделен сектор на местната икономика, както и върху общото производство. Така, експортно-ориентираните модели могат да бъдат класифицирани като входно-изходни модели само с два сектора.

11.1. Анализ „input-output”

Като използваме модела на Wassily Leontief за междуотрасловите връзки като негова основа, входно-изходния анализ може да се използва да се предвидят въздействията на ръста в търсенето в даден сектор върху останалата част от местната икономика. Ето как става това.

Входно-изходния анализ включва изграждането на квадратна n x n матрица. В тази матрица са записани всички потоци на продажбите (в редове) и покупките (в колони), които се реализират за една година при n местни производствени сектори, с други думи, междинните потоци на стоки (изразени в стойности) при различните сектори. Попълването на матрицата е в серии от колони и редове. Колоните са: продажбите от всеки сектор, крайното търсене (обществено и частно потребление, инвестиции и износ); редовете са покупките на първични факторите на производството, труда и капитала (и съответно възнагражденията и печалби) и покупките от чужбина и от друг регион (в случай на под-национално входно-изходна матрица) – внос.

Сумата на всеки ред представлява приходите на всеки сектор от продажби на стоки на други сектори и на крайни потребители. Сумата на всяка колона представлява разходите направени от всеки сектор, с цел да закупи стоки за междинно потребление и стоки, произведени извън него, и за заплащане на производствените фактори, заплатите и печалбите. Стойностите на редовете са равни на стойностите на колоните. Освен това, сумата от крайното потребление е равно на сумата от компоненти на дохода или на данък добавена стойност, като това е регионалната продукция Y (изход) (таблица 11.1).

С A_ij се обозначава стойността на стоките, които сектор i продава на сектор j, а C, G, I, Х и R – съответно обозначават личното потребление, държавните разходи, инвестициите, износа и стойността на продукцията.

 

Таблица 11.1: Структура на матрица за „input-output” анализ

 

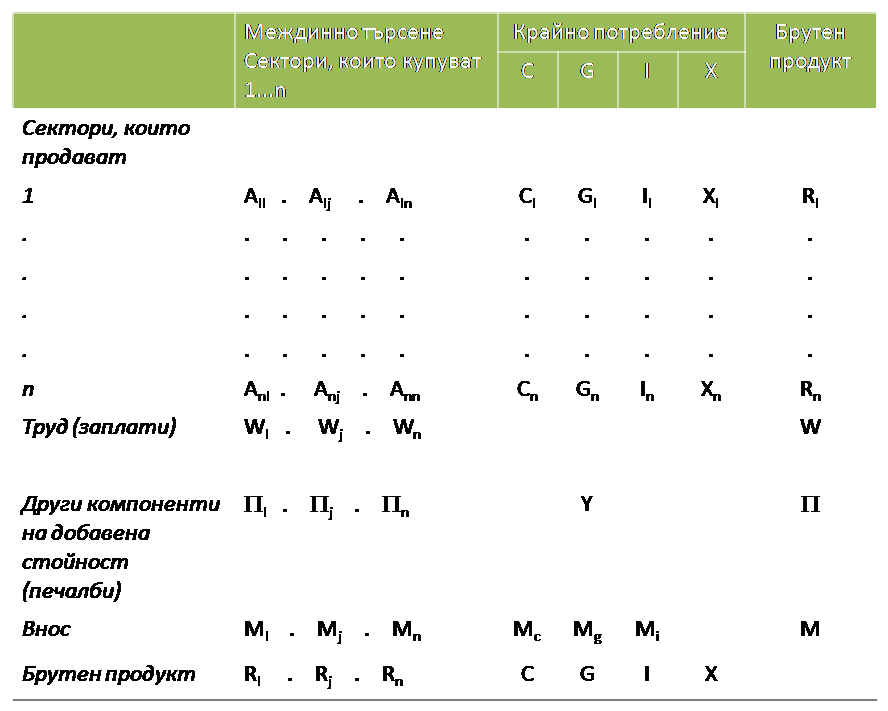
Потоците от стоки между сектор i и сектор j може да се изразят чрез т.нар. технически коефициент a_ij, който показва връзката (техническа/структурна) между производството на сектор i и сектор j. С други думи, техническият коефициент показва колко лева от сектор i са необходими, за да се постигне резултат от един лев в сектор j.

Input-output анализът е полезен инструмент за прогнозиране на ефектите от хипотетично повишение в търсенето при конкретен сектор. Ако се познава матрицата на техническите коефициенти е възможно да се изчисли ефекта на нарастване на външното търсене на една стока (сектор) ∆D_j върху:

• стойността на продукцията по отделни сектори i в региона
• заплатите в региона
• местната заетост, като приемаме постоянна средна работна заплата
• местния доход

 

Ограниченията на този метод са добре известни. На първо място, постоянството на техническите коефициенти спрямо увеличеното производство, както и постоянството им във времето, изисква цялото производство да бъде при постоянна възвръщаемост, и да няма техническия прогрес. Трудностите се увеличават, когато входно-изходния анализ се използва на под-национално, регионално и градско равнище. В този случай, ако инструментът се използва за прогнозиране на тенденциите в местната икономика, матрицата на техническите коефициенти трябва да бъде разделена на матрица на вътререгионален търговски поток и матрица на междурегионалния търговски поток. Това дава възможност за измерване на въздействието на увеличеното търсене в даден сектор върху местната икономика, и изключва „ефекти на изтичане” в други региони на страната. Но разделянето на матрицата на коефициентите по този начин е сложно начинание. Това обикновено се извършва с един от следните два метода: а) компилиране на таблици от емпирично изследване, което е точен, но изключително скъп метод; б) изследвания относно специализация като се предположи, че секторът е в състояние да отговори на повишеното търсене, само ако се касае за специализация на региона.

Използването на входно-изходния анализ за прогноза и симулиране въздействието на мерките на икономическата политика на местно ниво води до предположението, че техническите коефициенти са постоянни във времето. Следователно, резултатите от този анализ трябва да се интерпретират с повишено внимание.

11.2. Регион-вносител. Модел Harrod-Domar

Оригиналният модел

През 1939 г. икономистът Roy Harrod, а след това напълно независимо през 1957 г., Evsey Domar (снимка), изследват степента на растеж, необходим на една икономическа система, за да запази първоначалното си макроикономическо равновесие. Моделът, формулирани от Harrod и Domar заключава, че равновесието на една икономическа системата е по-скоро изключение, отколкото правило, тъй като пътят на икономически растеж е нестабилен и е много вероятно да се отклони от пътя на равновесния растеж.

Моделът Harrod-Domar по-късно се използва за интерпретиране на динамиката на регионалните икономически системи. Предположението, зад тази регионална версия е, че вносът (когато е анализиран като канал, по който капиталовите стоки и спестяванията са получени от други региони) определя темпа на растеж на местните икономики. Нещо повече, позволяват се равновесните условия за растеж да са по-малко рестриктивни (и следователно по устойчиво във времето) от тези, които се прилагат към националната икономика, близки до външната търговия. Следователно, докато експортно-ориентираната теория дава тежест на важността на външното търсене като двигател на развитие, моделът Harrod-Domar подчертава, че регионалната динамика може да бъде движена от инвестиции с произход от други региони, които стимулират местното производство и доходи – това са случаи (в) (г) и (д) представени в тема 10.

Както ще видим, моделът Harrod-Domar се различава от експортно-ориентираната теорията по това, че е модел, който може да обхваща много периоди. Той изоставя логиката на краткосрочния период, която видяхме дотук и приема по-дългосрочна перспектива. Нещо повече, далеч от разглеждане на спестяванията като намаление на ефективното търсене, този подход подчертава значението на спестяване в средствата, с които да се придобият ресурси за производствени инвестиции.

Едно нарастване на съвкупното търсене води до увеличение на капитала и труда, необходими за адаптиране на производството към ново ниво на потребление. Ако приемем пълна заетост, за да се поддържа това условие за равновесие, при хипотезата за постоянство на техническите производствени коефициенти (L/Y), темпът на нарастване на труда трябва да бъде равен на прираст на населението, n.

От гледа точка на капитала, увеличение в търсенето генерира увеличаване на инвестициите, чието финансиране изисква размер на спестяванията (S) равен на необходимите инвестиции (I). Ако случаят е такъв, икономиката расте при темп известен като „гарантиран темп на растеж" (y_t). Темпът на растеж трябва да бъде равен на съотношението между тенденцията да се пести s и коефициента на ускорение v, който от своя страна трябва да бъде равен на темпа на растеж на работната сила. Ако случаят е такъв, първоначалното равновесие между агрегираното търсене и производството ще се запази във времето.

Ако обаче системата расте, при гарантиран темп на растеж y_t , тя се придвижва, според писаното от Harrod, по протежение на „ръба” между рисковете от взрив, от една страна, и на рецесия от друга. Всяко неравновесие, генерирано от условия, външни за системата, при отсъствие от на външни интервенции, се влошава от сигналите от пазара, което кара фирмите да работят в посока, обратна на необходимата за възстановяване на равновесието. В една икономическа система, планираните инвестиции, надхвърлящи реалните икономии (I>S) сигнализира, че ефективното потребление е по-голямо от очакваното спестяване и следователно това ефективно търсене е по-голямо от очакваното търсене. Фирмите реагират на недостига на стоки в системата чрез увеличаване на инвестициите си – една реакция, която, парадоксално, влошава още повече неравновесието. Увеличаването на инвестициите генерира, чрез мултиплициращ ефект върху доходите, надпропорционално нарастване на доходите и агрегираното търсене. Последното все повече се отклонява от очакваното търсене, с тежки инфлационни ефекти в дългосрочен план. По същия начин, ако планираните инвестиции са по-малко от ефективното спестяване (I<S), това сигнализира, че очакваното търсене е по-голямо от ефективното търсене. Фирмите реагират на излишъка на предлагане чрез намаляване на инвестициите си, като по този начин забавят растежа на ефективното търсене, дори за дългосрочен период предизвикавайки рецесия.

Накратко, моделът показва, че има сили в икономическа система при първоначално неравновесие, които го тласкат все повече от статичното и в съответствие с първоначалните условия или към инфлация, или към дълбока рецесия.

Регионален вариант на модела

Когато моделът на Harrod-Domar се приложи на регионално равнище, той води до интересни резултати. Разликата тук е макроикономическото условие за равновесие, което за регионалната икономика става:

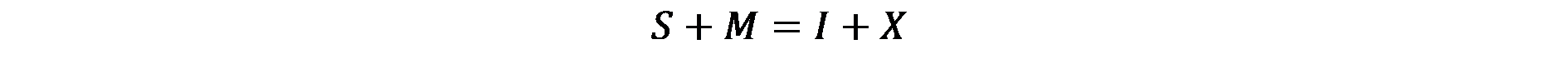 (11.1)

Където M и X съответно показват вноса и износа на капитал от/към един регион. Регионите не са близки икономически системи (ако те бяха, то регионалният модел не би се различавал от националния), те имат тесни връзки с други региони, с които те обменят блага и производствени фактори.

За разлика от затвореното стопанство) капиталът може да расте със същия темп както резултата (така гарантирайки стабилно състояние) дори, ако инвестициите изпреварват спестяванията. Така разминаването между спестявания и инвестиции се покрива от излишъка на нетния внос. Регионалната икономическа система може да финансира инвестиции не само от вътрешни спестявания, но чрез внос на капиталови стоки от други региони. По същия начин нетният износ може да помогне за поддържане на стабилното равновесие, когато има излишък на вътрешни спестявания, защото те изглаждат дефицита между ниското вътрешно потребление и нивото на производството кореспондиращо с пълното използване на производствения капацитет.

По същия начин, пълната заетост в един регион с вътрешен недостиг на труд може да се поддържа чрез поток от работници от други региони, докато потоци от мигранти към други региони може да компенсира безработицата в региона.

Първият важен резултат получен от регионалния вариант на модела на Harrod—Domar е, че условията за постоянен темп на растеж не са така рестриктивни (и затова по-устойчиви във времето) отколкото тези ръководещи една национална икономика близка до чуждестранна търговия. Стабилното равновесие може да се приеме като изключение, а не като правило, при отсъствие на условия в модела осигуряващи междурегионални потоци от труд и капитал за гарантиране на икономически растеж при постоянен темп. Това означава, че в модела няма условия, които гарантират, че междурегионални потоци от производствени фактори ще уравновесят системата.

Вторият важен резултат от регионалния вариант на модела е, че региони, които се характеризират от нетен излишък от внос са тези, които

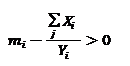 (11.2)

растат по-бързо от другите – тенденцията да се спестява и отношението капитал/резултат остават равни. Според логиката на модела, нетният излишък на вноса расте при по-висок темп на растеж, защото този излишък представлява допълнително спестявания внесени в икономическата система отвън.

Накрая, третият важен резултат от модела на Harrod-Domar се отнася до тренда на разликите между темповете на растеж на регионите. Ако има първоначални разлики между темповете на растеж при регионите, моделът показва, че тези разлики не само перзистират, но и нарастват с времето.

Тези констатации ни напомнят (при реалистичното предположение, че един беден регион е нетен вносител на капитал от богатите региони), че моделът предполага сближаване по темпове на растеж при устойчиво равновесие. Темпът на растеж на един беден регион е постоянно по-висок от този при напредналите региони – ситуация, предизвикана от конвергентното развитие. Това показва, че, в условия характеризиращи се с недостатъчно склонност към спестяване (икономисване) и ниското отношение капитал/резултат (v) тенденцията да се внася играе основна роля в процеса на вътререгионално и международно възстановяване на равновесието.

По-голяма темп на растеж се постига от региони с висока склонността да спестяват и с ниско съотношение капитал/резултат (v), т.е региони, които ефективно използват капитала или имат ниска капиталово интензивна отраслови структури (например сектора на услугите). Последната характеристика позволи на италианската област Ломбардия постигане високи нива на развитие, въпреки дългогодишния нисък процент на натрупване (70-те и 80-те години на 20-ти век). За сметка на това Южна Италия, където са направени капитало-интензивни инвестиции в продължение на тридесет години (1955-85), е постигнало ограничен растеж, независимо от голямата инжекция на (публични) инвестиции и външни спестявания.

Това наблюдение ни дава възможност да кажем, че дори при кейнсиански модели, ако те приемат чисто динамична, многопериодна и дългосрочна перспектива, наличието на формиране на спестявания и капитал, т.е. елементи на предлагане а не на търсене, обяснява регионалния растеж.

Моделът на Harrod-Domar е много подходящ за описание и обяснение на развитието на регионалните икономически системи, характеризиращи се с критични макроикономически условия. Ограничените вътрешни спестявания, по-ниското съотношение капитал/резултат и отрицателното търговско салдо се очаква да възпрепятстват макроикономически растеж. Но тази ситуация е в противоречие с реалното състояние на много регионални системи, и това може да се обясни само ако се определи решаваща роля на външни капитали, което прикрива дефицита на вътрешни спестявания. Когато същата логика се използват за идентифициране на относителен растеж, тя е в състояние да отчита сближаващите се темповете на растеж на региони, които се различават значително в техните нива на вътрешните инвестиции и спестявания – нива, които иначе биха сигнализирали за дивергенция.

11.3. Неокласически модел на икономическия растеж

Въпреки че тук се отнасят теории, които те се различават по някои от своите предположения, тези теории включват широка основа от строго неокласически модели, които приемат различни хипотези относно мобилността на стоките и производствените фактори.

Дисбалансът в междурегионалната естествена осигуреност с производствени фактори, както и разликите в нивата на тяхната производителност, обяснява предимствата на местното/регионалното стопанство спрямо останалия свят. Това са елементите, които стоят в основата на пътя на растежа и които обуславят периода и формата, които той заема.

Според тези теории, търговията със стоки и/или производствени фактори обяснява установяването на определени относителни цени на стоки и фактори, повишаването на производствения капацитет и постигането на пълна трудова заетост.

Трябва да се отбележи, че понятието „икономически растеж” тук се използва с друго значение спрямо разгледаното в предишните теми. Причината за тази разлика в смисъла на понятието „растеж” е факта, че тези модели имат по-различни акценти на политиката – това не е ограничаване на високата безработица (чрез увеличаване на търсенето на местни стоки), а проблемите на бедността, недостатъчното развитие и неравенството в разпределението на доходите. Растежът следователно вече не се интерпретира като увеличаване на заетостта и краткосрочните доходи, а се разглежда като благополучие на отделната личност (и междурегионалната конвергенция), което се постига или чрез повишаване на факторната производителност (и съответно в заплатите и дохода на глава от населението – неокласически макроикономически модели), или чрез процесите на специализация, които генерират междурегионална търговия, и следователно предимствата, произтичащи от покупките на стоки, предлагани на външния пазар по цени по-ниски, отколкото биха били, ако стоките са произведени вътрешно.

Тези теории имат редица отличителни характеристики, които трябва да се имат предвид. Първата група теории – за факторната мобилност, използват понятието „относителен растеж”, като целта е да се идентифицира и да обясни пътя на конвергенция или дивергенция в нивата и темповете на растеж на производството. Отличителна черта на втората група теории – за междурегионална търговия – е, че те използват понятието „относително предимство”, или „сравнително предимство”, формулирано за първи път от Рикардо в неговия класическия модел по международната търговия и въз основа на които става възможно да се определи специализацията на региона. Сред всички стоки, които могат да бъдат предложени на външния пазар, регионът изнася тези, които произвежда при сравнително по-ниски производствени разходи. Тази разлика в производствените разходи се дължи на различната производителност на факторите, използвани за производството на стоките. Това означава следното – дори ако един регион произвежда всички стоки на по-високи цени, така че по принцип има по-неефективен производствен процес от всеки друг регион в страната, той може все пак да бъде сравнително по-малко неефективен при производството на определена стока. Регионът ще може да получи роля в международното разделение на труда като се специализира в производството на стоката, при която е относително по-ефективен. Прилаганите подходи са подходи, използват концепцията „еднородно абстрактно пространство”, за да се разглеждат икономическите условия, по отношение на общите икономически показатели.

Най-новите теоретични разработки в областта на икономическия растеж и все по-големият достъп до регионални данни водят до все по-засилен интерес към различията в регионалния икономически растеж. Основният тласък на този интерес идва от опитите да се подобри прогностичната способност на т.нар. неокласически модел на икономическия растеж, чието начало се поставя от американския икономист Robert Solow, удостоен с Нобелова награда за икономика през 1987 г., за публикациите му през 1956 и 1957 г. Други американски икономисти стават пионери в по-нататъшни теоретични разработки на неокласическия подход към икономическия растеж и тези по-нови теории са тествани имено към регионални данни.

Целта е да се обяснят основните елементи на неокласическия модел и да се направи преценка за неговата приложимост към съществуващите междурегионални различия. Макар че икономическият растеж е изследван от поколения икономисти, все още има несъгласия относно неговите основни причини. Това се илюстрира ясно при съвременните проучвания на междурегионалните различия в икономическия растеж. Някои учени следват неокласическия път, подчертавайки ролята на предлагане на производствени фактори при икономическия растеж. Техническият прогрес се приема за двигател на растежа и определя темпа на нарастване на производителността на труда (продукта/1 работник) в дългосрочен период. Като се дава тежест на технологичния прогрес в неокласичесическия модел на растежа, усъвършенстването на този модел през последните години се основава на обяснения относно как да бъдат измерени технологичните промени. Защитниците на усъвършенствания неокласически модел на икономическия растеж разработват т.нар. ендогенен модел на икономически растеж. Тази по-нова теория за икономическия растеж твърди, че техническият прогрес е едновременно причина и резултат на растежа и много усилия се полагат за анализиране на последиците от радикалното разширяване на първоначалния модел на Solow.

Икономическия растеж без технологични промени

Агрегираната производствена функция стъпва на основата на неокласическия модел на икономическия растеж. При икономика без технически прогрес, продуктът се определя изцяло от факторите капитал и труд.

Функцията пък на един човек показва, че продуктът на 1 работник (производителността) може да нараства само, ако капитала на 1 работник нараства. С други думи, капиталът трябва да расте по-бързо отколкото труда, за да нараства продукта на 1 работник. Тази положителна връзка между капитала на 1 работник и продукта на един работник е показан наПродуктът на 1 работник ще нараства, когато нараства оборудването на 1 работник – процес известен като capital deepening – но нарастването ще бъде при намаляващ темп, поради намаляващата маржинална възвръщаемост. Нещо повече, когато маржиналния продукт от труда спадне до определено ниво, нетните инвестиции (брутните инвестиции минус амортизацията) ще спаднат до нула, т.е брутните инвестици ще бъдат достатъчни само да поддържат наличния капитал.

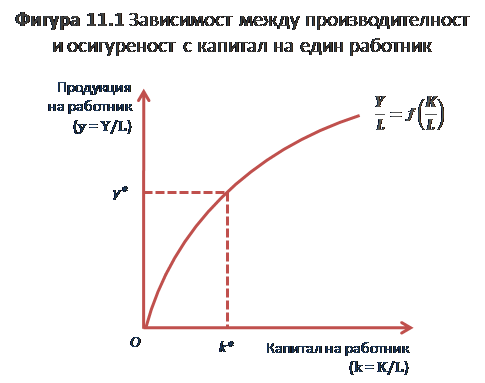
Съотношението капитал/труд е в своето дългосрочно равновесие в точка k*. Това равновесно съотношение капитал/труд е свързано със съответното равновесно равнище на продукта на 1 работник y*. Щом се достигне това равновесие, няма да има стимул за производителите да увеличават стойността на отношението капитал/труд. Тъй като двете отношения капитал/труд и продукт/труд са константни при това равновесие, то икономиката е в дългосрочно равновесие.

Едно по-пълно разглеждане на неокласическия модел показва, че равновесното отношение капитал/труд се определя отчасти от производствената функция и отчастиот друга функция определяна като фундаментално уравнение на растежа. Последното показва, че отношението капитал/труд ще продължи да расте когато брутните инвестиции на 1 работник надхвърлят това ниво, което: 1) е нобходимо за заместване на износеното оборудване и 2) осигурен е допълнително капитал за нарастналата работна ръка.

При това най-просто представяне на неокласическия модел може да не отчете нарастване на дохода на глава от населението в дългосрочен план тъй като дългосрочното равновесие се определя като ситуация, при която продуктът, капиталът и труда нарастват с един и същи темп. Има възможност за нарастване на продукта на 1 работник, но в средносрочен план.

Нарастването на дохода на глава от населението ще се постигне в средносрочен период при условието за дългосрочно равновесие – капиталът и труда да нарастват с еднакъв темп.

Заключения:

• Брутният продукт нараства неограничено, когато предлагането на капитал и труд нарастват
• Продуктът на 1 работник може да нараства само, ако има т.нар. капиталова интензивност (отношението капитал/труд нараства)
• Когато отношението капитал/труд достигне своето дългосрочно равновесие, няма да има по-нататъшен ръст на продукта на 1 работник.

Икономическия растеж при технологични промени

Повече реализъм се внася в неокласическия модел като се отрази ефекта от технологичните промени върху нарастване на продукта. Най-удобният начин за отразяване на технологичния прогрес е да отчетем техническото познание като отделен елемент в производствената функция. Приема се, че трудът и капитала имат една и съща полза от техическия прогрес.

Този начин на представяне на влиянието на техническия прогрес върху нарастване на продукта е опростен, защото игнорира вероятността техническият прогрес да е основан на допълнително капитал чрез инвестиции в последно закупените машини. Работната ръка също ще придобие нови знания и умения, по такъв начин увеличавайки ефективността на работниците във времето, при което трудът, както и капиталът трябва да бъде коригиран съобразно „качеството” си.

Независимо от проблемите при моделирането на начина, по който техническия прогрес въздейства върху нарастването на брутния продукт и продукта на 1 работник, ясно е че техническият прогрес има изключително значение за икономическия растеж. Влиянието на техническия прогрес върху продукта на 1 работник е демонстриран наИзместването нагоре на продукта на 1 работник в резултат от техническия прогрес води до повишаване на продукта на 1 работник при всяко равнище на съотношението капитал/труд.

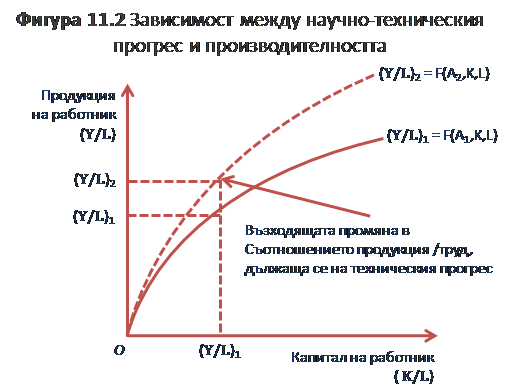
Разширеният вариант на неокласическия модел е привлекателен с това, че позволява стабилен растеж на продукта на 1 работник за дълъг период. Така дори, ако капиталът и трудът нарастват с един и същи темп, продуктът на 1 работник ще нараства при условие, че равнището на техническият прогрес е по-голямо от нула. При дългосрочно равновесие, приемаме, че нарастването на продукта и на капитала е едно и също (∆Y/Y=∆K/K).

Тази кратка дискусия върху неокласическия модел на икономическия растеж включва достатъчна основа за да се оцени потенциала за прилагането му при обясняване на регионалните различия в икономическия растеж. Регионалният модел на икономически растеж дава информация откъде произтичат регионалните различия в икономическия растеж:

• Техническият прогрес може да е различен при отделните региони
• Нарастването на капитала може да варира при отделните региони
• Нарастването на работната сила може да варира при отделните региони.

Равнището на техническия прогрес може да варира при различните региони. Регионалните различия при нарастване на продукта на 1 работник се обясняват с регионалните различия в техническия прогрес и с регионалните различия в нарастване на съотношението капитал/труд.

Определяне компонентите на икономическия растеж

Неокласическият модел идентифицира три източника на нарастване на продукта – наличния капитал, работната сила и технологията. Следователно регионалният икономически растеж на продукта ще зависи от темпа на нарастване на тези три производствени фактора. Преди да разгледаме източниците на икономическия растеж, ще бъде полезно да изследваме причините, поради които нарастването на капитала, труда и технологията могат да са различни при отделните региони.

Един потенциално важен фактор за междурегионалните различия е междурегионалната миграция на факторите. Според неокласическия модел, капиталът и трудът ще се придвижват към тези региони, които предлагат най-висока възвръщаемост за тях. Производителите ще търсят най-печелившите локализации за техните предприятия и машини, а работниците ще бъдат привлечени към тези региони където има високо заплащане на труда. Неокласическият модел приема, че няма пречки за междурегионалната факторна мобилност и че има съвършена информация относно цените на факторите във всички региони. Регионалните различия са резултат не само от регионалните различия по отношение на присъщите за всеки регион темпове на нарстване на капитала и труда, но също и от междурегионалната миграция на производствените фактори.

Фигура 11.3 Цикъл на нарастване на спестяванията

На фигура 11.3 са отразени тези процеси. Фигурата демонстрира набора от фактори, които се очаква да повлияят върху нарастването на капитала, труда и технологиите в един отделен регион. Нарастването на наличния капитал например зависи от инвестициите на населението и от входящите капиталови потоци от други региони. Тези два фактора са зависими, съответно от равнището на спестяванията на населението на региона и възвръщаемостта на капитала в съответния регион в сравнение с другите региони. Оттук, нарастването на продукта ще бъде по-бързо ако нарастват спестяванията, тъй като това ще доведе до по-бързо нарастване на наличния капитал чрез нарастване на размера на инвестициите за периода. Подобни аргументи можем да приложим за нарастване на работната сила, която ще зависи не само от нарастване на населението, но и също от нетната имиграция от други райони.

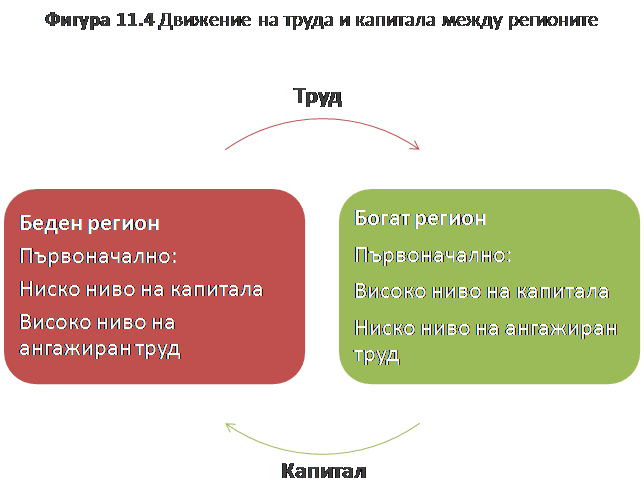
При кои региони се очаква да има най-бърз икономически растеж, при условие, че капиталът и трудът са съвършено мобилни? Според неокласическия модел, регионите с по-висока стойност на съотношението капитал/труд ще имат по-високи заплати и ниска доходност от инвестициите. Това ни води до прогнозата, че капиталът и трудът ще се движат в обратна посока: регионите с висока стойност на съотношението капитал/труд ще се характеризират с имиграционни потоци на работна ръка и изходящи потоци на капитал и обратно при региони с ниска стойност на съотношението капитал/труд. С други думи, регионите с ниски заплати ще привличат капитал и ще губят работна ръка, а региони с високо равнище на заплатите ще привличат работна сила, а ще губят капитал (Фигура 11.4). Не е възможно обаче да се прогнозира дали икономическият растеж ще бъде по-висок в регионите с ниски заплати или в тези с вискоко заплащане на труда, тъй като растежът зависи от скоростта, с която капиталът се влива в региона с ниски заплати спрямо скоростта, с която работната сила изтича от този регион. Ако капиталът е по-мобилен от труда (което е много вероятно) регионите с ниско равнище на заплащането ще имат по-бърз икономически растеж, тъй като капиталът ще се придвижва към този регион по-бързо отколкото изтича работната сила.