1.Строеж и свойства на течности. Повърхностно напрежение. Капилярни явления.
1.1. Особености на молекулния строеж на течностите.
Течностите по своя строеж заемат междинно място между твърдите тела и газовете. При течностите не можем да говорим за хаотично движение на молекулите като при газовете, но и липсва подредено състояние като при кристалните вещества. При тях съществува т.н. подреденост от близък порядък (Фиг 1.1). Това означава, че по отношение на дадена молекула най-близките около нея молекули са разположени подредено, на тази подреденост се губи по отношение на далечните молекули.
Фигура 1.1. Подреденост от далечен и близък порядък.
Молекулите на течностите, подобно на частиците на твърдите тела, трептят около дадено равновесно положение известно време, след това със скок преминава в ново равновесно положение. Средното време, което молекулите пребивават в дадено равновесно положение, се нарича време на релаксация. То зависи от температурата и налягането. С повишаване на температурата това време намалява и това повишава подвижността на течностите.
Течностите обикновенно са изотропни, т.е. свойствата им са еднакви във всички направления. Изключение от това правило се наблюдава само при т.н. течни кристали, които са изградени от молекули с удължена форма, и в определен температурен интервал се характеризират с по-висока степен на подреденост.
Разстоянието между частиците на течностите са малки (от порядъка на 10-10 m) и поради това те са малко свиваеми и имат голяма плътност.
Тъй като междумолекулните сили на взаимодействие зависят от разстоянието, то реално всяка молекула взаимодейства само с тези, които се намират на разстояние, равно на радиуса на молекулно взаимодействие, който е равен на 1.5 10-9 m. Около всяка молекула може да се опише сфера с този радиус, наречена сфера на молекулно взаимодействие. Следователно една молекула ще взаимодейства само с тези молекули, които са вътре в тази сфера.
1.2. Свойства на повърхностния слой на течността. Молекулно налягане. Повърхностно напрежение.
Нека имаме молекула А, коята се намира на достатъчно разстояние от повърността на течността и от стените на съда (Фиг. 1.2). Тогава от всички страни тази молекула ще я обкръжават средно еднакъв брой други молекули. Следователно резултантната сила, която действа на избраната молекула, ще бъде равна на нула.
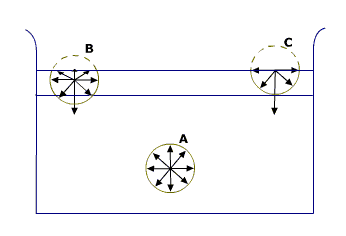
Фиг. 1.2.
Нека имаме молекула С, която се намира на повърхността на течността. Тогава в сферата на молекулно взаимодействие ще влизат молекули както от течността, така и от газовата фаза над течността. В газовата фаза концентрацията на частиците е много по-малка, отколкото при течностите. Поради това резултантната сила, която действа на молекулата ще бъде различна от нула и ще бъде насочена навътре към течността, перпендикулярно на свободната повърхност. Подобна сила ще действа и на молекулата В. Следователно молекулите от повърхностния слой на течността, с дебелина равна на радиуса на молекулното взаимодействие, действат със сили върху по-долните слоеве на течността. Тези сили, отнесени за единица площ от свободната повърхност, се наричат молекулно налягане. Това налягане може да има високи стойности, например за водата е около 1010 Ра. Под неговото действие течностите се оказват свити, което обяснява малката им свиваемост под действието на външни сили.
Тъй като молекулите от повърхностния слой действат върху по-долните с определена сила, то те притежават допълнителна потенциална енергия. Следователно течностите ще имат минимум потенциална енергия, когато те приемат форма, при която имат най-малка повърхност, а това е сферичната форма. Когато на една течност действа и друга сила, например силата на тежестта, тя заема форма, съответствуваща на минимум на пълната енергия. В най-често срещаният случай това е формата на съда, в който се намира течността.
Повърхността на течността може да се оприличи на еластична ципа, която се стреми да се свие, за да намали повърхностната си енергия. Поради това на граничния контур, който ограничава течността, действат сили, перпендикулярни към контура и допирателни към повърхността на течността (Фиг. 1.3.). Тези сили се наричат сили на повърхностно напрежение.
Фиг. 1.3.
Силата на повърхностно напрежение, която действа на контур с дължина единица, се нарича коефициент на повърхностно напрежение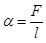 
. Измерва се в единици N/m.
Поради тези свойства на повърхностния слой на течностите е възможно някои насекоми да се движат по повърхността на течностите или малки предмети да е задържат върху нея, както е показано на снимките (Фиг. 1.4.).
Фиг. 1.4.
Коефицентът на повърхностно напрежение зависи от естеството на течността, от температурата и от примесите в течността. С повишаване на температурата коефициентът на повърхностно напрежение намалява, а с понижаването на температурата се повишава. Примесите в течността могат да влияят по два начина. Вещества, които намаляват повърхностното напрежение се наричат повърхностно активни. По отношение на водата това са спиртът, етерът, сапунът и други вещества. Някои вещества увеличават повърхностното напрежение на течностите. Те се наричат повърхностно пасивни.
Увеличаването на свободната повърхност на течност може да стане само ако молекули от вътрешността на течността излязат на повърхността, тъй като при течностите не може да стане увеличаване на разстоянията между молекулите. Тъй като повърхностният слой упражнява върху по-долните слоеве от течността молекулно налягане, то за да излязат молекулите от вътрешността на течността на повърхността те трябва да извършат работа за да преодолеят тези сили. Коефицентът на повърхностно напрежение може да се дефинира и чрез работата, която трябва да се извърши, за да се увеличи свободната повърхност с единица.
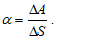
При това нараства повърхностната потенциална енергия на течността за сметка на кинетичната енергия на частиците на течността, т.е. температурата на течността ще се промени. Обратният процес става при намаление на свободната повърхност. Онази част от повърхностната потенциална енергия, която може да се превърне в работа при изатермично намаление на повърхността на течността се нарича свободна енергия на повърхността.
.
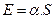1.3. Молекулно налягане под изкривена повърхност.
Стойността на молекулното налягане зависи не само от естеството на течността, но и от формата на повърхността и. Когато повърхността на течността не е равнинна, стремежът и да се свие предизвиква появата на допълнително налягане.
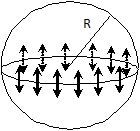
Фиг. 1.5.
Нека имаме една сферична капка с радиус R и мислено да я разделим на две полусфери по една от диаметралните и равнини. Поради повърхностното напрежение на граничният контур ще действа сила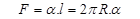 
. Тази сила обуславя допълнително налягане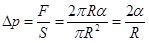 
Тази формула се нарича закон на Лаплас за допълнителното налягане под изкривена повърхност.
Посоката на това допълнително налягане е към центъра на кривината на повърхността. При изпъкнала повърхност то увеличава налягането на повърхностния слой, а при вдлъбната повърхност го намалява (Фиг. 1.6.).
Фиг.1.6.
При попадане на мехурче въздух или газ в кръвоносен съд, то може да го запуши. Това се нарича емболия. Причина за придвижването му е деформирането му вследствие на допълнителното налягане от кръвта, която го обтича. Поради това радиусът на кривината на предната и задната му част стават различни и сумарната разлика в налягането е насочена срещу движениета на течността. Въздушно мехурче може да попадне в кръвоносен съд при нараняване на голяма вена, а газово мехурче може да се появи при рязко изменение на налягането, например бързо изкачване от голяма дълбочина на водолаз.
1.4. Явления на границата между течност и твърдо тяло.
На границата на течност и нейните наситени пари, две несмесващи се течности, течност и твърдо тяло или твърдо тяло и газ възникват сили, обусловени от различните междумолекулярни взаимодействия на граничещите среди. Силите на взаимодействие между еднородни молекули се наричат кохезионни, а между разнородни молекули – адхезионни.
Нека имаме капка течност, намираща се на повърхността на твърдо тяло (Фиг. 1.7. ).
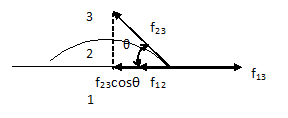
Фиг. 1.7.
Системата ще има конфигурация, която съответства на минималната сумарна потенциална енергия. На единица дължина от граничната линия между течността и твърдото тяло ще действат 3 сили f12, f23 и f13, чиято големина ще бъде равна на съответните коефициенти на повърхностните напрежения α12, α23 и α13. Ако капката е в равновесие, векторната сума от всички действащи сили трябва да бъде равна на нула. Проектирайки тези сили по направлението на повърхността на твърдото тяло и замествайки силите със съответните коефициенти на повърхностни напрежения ще получим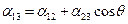 
, където θ е ъгълът между допирателната към повърхността на течността и повърхността на твърдото тяло. Нарича се граничен ъгъл (ъгъл на мокрене). От горната формула за стойността на граничният ъгъл се получава 
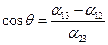. При α13- α12=α23, междумолекулните сили са напълно компенсирани и θ=00. В този случай капката се разтича по повърхността на твърдото тяло и имаме пълно мокрене. При θ=1800 имаме пълно немокрене. Течността се допира до твърдото тяло само в една точка. Капка от немокреща течност има формата на повече или по-малко сплесната сфера (Фиг. 1.8).
Фиг. 1.8.
Мокренето и немокренето са относителни свойства. Например водата мокри стъклото, но не мокри парафина. Живакът не мокри стъклото, но мокри желязна повърхност.
1.5. Капилярни явления.
Поради съществуването на граничен ъгъл в тесни капилярни тръбички или в процепи между две стени изкривяването на повърхността на течността може да обхване цялата повърхност на течността. Такива изкривени повърхности се наричат мениски. Ако течността е мокреща за повърхността на капилярката, повърхността и ще бъде вдлъбната, а ако е немокреща – изпъкнала. Изпъкналата или вдлъбнатата повърхност променя (увеличава или намалява) молекулното налягане на повърхността. В резултат на което при мокреща течност тя ще се издигне на някаква височина над нивото на течността в широката част на съда, а при немокреща течност нивото на течността в капилярката ще бъде по-ниско (Фиг. 1.9). Височината, с която се променя нивото на течността в капилярката, се нарича капилярно повишение или намаление.
Фиг. 1.9.
Нека цилиндрична капилярна тръбичка с радиус r се потопи в течност, която я мокри (Фиг. 1.10). Тогава вдлъбнатата свободна повърхност ще намали налягането на повърхностния слой на течността и тя ще се издигне на някаква височина в тръбичката
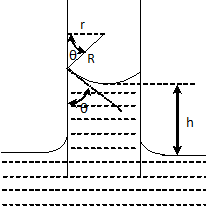
Фиг.1.10.
Тази височина ще бъде такава, че хидростатичното налягане на стълба течност с височина h да компенсира намалението на налягането поради изкривената повърхност. Следователно
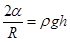
Радиусът на изкривената повърхност R, разглеждана като част от сфера, може да се изрази чрез радиуса на капилярката r и пристенния ъгъл θ
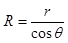
Замествайки в горната формула, получаваме за h
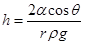
Тази формула е валидна и за случаите на капилярно понижение и се нарича формула на Журен. В много тънки капилярки течността се издига на голяма височина. Например за тръбичка с диаметър d=0.5 μm водата при условие на пълно мокрене се издига на височина около 30 метра.
Капилярните явления играят голяма роля в природата и практиката. Поради капилярни явления порести вещества могат да задържат значително количество течност, което води до увлажняване, например на памучни влакна и памучни тъкани във влажни помещения, задържане на влага в почвата, изкачване на хранителни вещества по стъблата на растенията и т.н. Обратно, немокрещи течности не проникват в порести тела. Например перата на птиците, смазани с мазнина, са напълно непроницаеми за водата.
