11. Хидродинамика. Закон на Бернули за стационарно и ламинарно движение на идеална течност. Движение на течност по тръби с твърди и еластични стени. Пулсова вълна. Пулсова честота.

Начинът на движение на течностите се определя както от някои свойства на течностите, така и от външните условия – скорост на движение, радиус на тръбата, в която се движи и др. От параметрите, характеризиращи течностите, начинът на движение се определя главно от плътността и вискозитета на течностите. При някои процеси можем да пренебрегнем въздействието на някои свойства на течностите, например да считаме, че те са несвиваеми и вискозитета им е пренебрежимо малък. Такава течност, която е несвиваема и невискозна, се нарича идеална течност. 

11.1. Начини за описание на движение на течностите.

За онагледяване на движението на течностите се въвеждат понятията “частица на средата” и “токова линия”. Частица на средата е малък обемен елемент от течността с линейни размери, многократно по-големи от междумолекулните разстояния. Характерът на движение на течността можем да определим като проследим движението на една частица на средата. Линия, във всяка точка на която допирателната съвпада с посоката на скоростта на частицата, се нарича токова линия. Токовите линии се чертаят така, че гъстотата им да характеризира големината на скоростта. В областите с по-голяма скорост токовите линии се сгъстяват.

Движение, при което токовите линии не се пресичат, се нарича ламинарно или слоисто (Фиг. 11.1). Движение, при което токовите линии се пресичат, се нарича турбулентно (вихрово).

Движението може да преминава от ламинарно в турбулентно и обратно. Това става когато определена комбинация от величини е над дадена критична стойност, която се нарича число на Рейнолдс 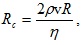където R – радиуса на тръбата, по която се движи течността, ρ – плътността, v – скоростта, η – вискозитета на течността.

11.2. Уравнение за непрекъснатостта на струята.

Ако имаме една реална тръба или т.н. токова тръба, ограничена от няколко токови линии (Фиг. 11.2), то обемът на течността, която преминава през напречното сечение за единица време се нарича поток на флуида Ф.

Ф = S.v

Ако течността е несвиваема, то през всяко сечение трябва да премине еднакъв поток. Следователно:

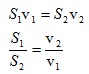
т.е. скоростите на течността са обратно пропорционални на сеченията, през които тя преминава. Това уравнение се нарича уравнение за непрекъснатостта на струята.

Фиг. 11.2.

11.3. Уравнение на Бернули.

Нека имаме нехоризонтална реална или токова тръба с променливо сечение и в тази тръба имаме идеална течност с плътност ρ (Фиг. 11.3). Под действие на външна сила течността се премества. Нека в момент t₁ течността преминава през сечение S_1, а в момент t₂ през сечение S₂.

Фиг. 11.3.

Работата  А на външната сила, преместваща течността, ще доведе до промяна в нейната кинетична и потенциална енергия.

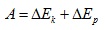
Изменението на кинетичната и на потенциалната енергия на течността ще бъдат съответно:

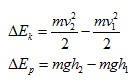
Резултатната работа за преместване на течността ще бъде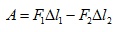

Ако заместим силата с произведението на налягането и площта на тръбата, то ще получим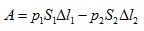

Произведението на сечението S и преместването Δl дава обема течност, преминаващ през тръбата за единица време. Тъй като течността е идеална, т.е. несвиваема, то колкото течност преминава през сечението S_1, толкова ще премине и през сечението S₂. Следователно 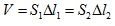 и формулата за работата можем да запишем във вида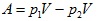

Масата на течността можем да изразим чрез плътността и обема на течността m=ρV. Тогава формулите за изменението на кинетичната и потенциалната енергия ще придобият вида:

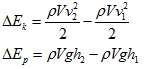
Ако заместим във формулата за работата с равните им, ще получим:

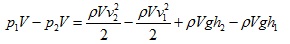
Разделяйки на обема на течността и групирайки членовете с еднакъв индекс получаваме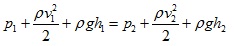

Тъй като моментите t₁ и t₂ са избрани произволно, то за всяко сечение на тръба, когато по нея тече стационарен поток на идеален флуид, ще бъде изпълнено уравнението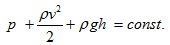

Това съотношение се нарича уравнение на Бернули. То изразява закона за запазване на енергията при движение на идеална течност, т.е. пълната енергия на идеална течност за единица обем е постоянна величина. Във формулата p се нарича статично налягане, 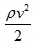- динамично налягане и 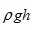- хидростатично налягане. Сумата от тези три величини се нарича пълно налягане 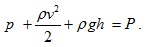. При движение по хоризонтална тръба уравнението на Бернули ще има вида 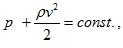тъй като 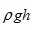също ще бъде равно на константа.

11.4. Методи за измерване на налягането.

Статично налягане е налягането, с което течността действа върху повърхността на телата, които тя обтича. Може да бъде измерено с тръбичка, която има отвор на страничната повърхност (Фиг. 11.4). Статичното налягане в точка М ще бъде равно на хидростатичното налягане на стълба течност във вертикалното коляно на тръбичката, т.е. по височината h на стълба течност във вертикалното коляно на тръбичката можем да съдим за статичното налягане.

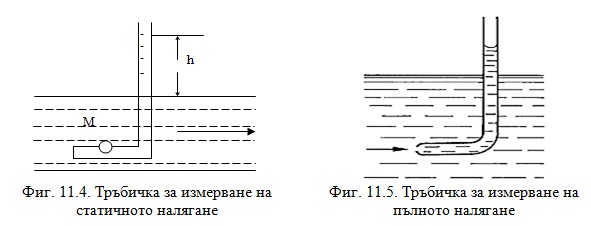
Пълното налягане се измерва с тръба, с отворен преден край на хоризонталното коляно (Фиг. 11.5). Течността, която влиза в тръбичката се спира и по височината на стълба течност във вертикалното коляно на тръбата можем да съдим за пълното налягане на течността.

Динамичното налягане зависи от скоростта на течността. В местата, където течността спира, се получава допълнително налягане 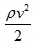. Динамичното налягане се измерва с тръба на Пито, която е комбинация от тръбите за измерване на пълното и на статичното налягане. По разликата в нивото на течността в двете тръбички можем да съдим за динамичното налягане.

11.5. Прибори, действието на които се обяснява със закона на Бернули

От уравнението на Бернули и уравнението за непрекъснатостта на струята следва, че в местата на стеснение на тръбата скоростта на движение на течността нараства и следователно динамичното налягане се увеличава, а статичното намалява. Възможно е при определено съотношение на скоростта на течение и сечението на тръбата в стеснения участък статичното налягане да стане по-малко от атмосферното и ако в този участък се пробие дупка от нея да не изтича течност, а да се всмуква въздух. Това явление се използва за обяснение на действието на уреди като тръба на Вентури, пулверизатор, водна помпа, карбуратор и др.

Пулверизаторът служи за разпрашване на течности. Представлява съд за течност с две тръбички, поставени под прав ъгъл (Фиг. 11.6). С ръчна гумена крушка или помпа се създава струя въздух с голяма скорост. Това създава намалено статично налягане над отвора на втората тръбичка, потопена в течността. Течността се изкачва по тръбичката и се разпрашва от силната въздушна струя в хоризонталната тръба. Пулверизирането на различни течности се използва широко в медицината, растителната защита, промишлеността и бита.

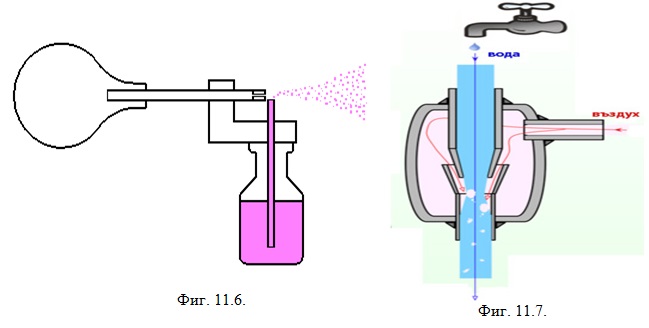
Водната помпа се състои от стъклен съд, в който има запоени 3 тръбички. Едната тръба (1) има на края си стеснение (Фиг. 11.7). През нея се пуска вода под налягане. Водната струя излиза от стеснението на първата тръба с голяма скорост. Поради това статичното налягане при излизане от тръбата рязко намалява и се засмуква въздух от съда 2. Въздухът заедно с водата изтичат през тръбата 3. Водната помпа има краен вакуум около 13.3 кРа.

Тръбата на Вентури служи за определяне на скоростта и потока на флуид (Фиг. 11.8). По дължината на тръбопровода се монтира специален участък с две различни по големина калибрирани сечения. В тези две сечения се измерва статичното налягане Р₁ и Р₂.

Фиг. 11.8.

Прилагайки уравнението на Бернули за двете сечения S₁ и S₂ получаваме:

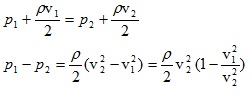
От уравнението за непрекъснатостта на струята следва, че 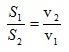и следователно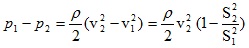

Знаейки плътността на течността и сеченията на тръбата S₁ и S₂ и измервайки разликата в налягането в двете колена на манометричната тръба р₁-р₂ можем да намерим скоростта v₂, а оттам и потока на флуида през тръбата.

11.6. Движение на реална течност по хоризонтална тръба с постоянно и променливо сечение.

При движение на реална течност възниква съпротивление при движение, породено от триенето между стените на тръбата и течността (външно триене) и триене между отделните слоеве на течността (вътрешно триене). Тъй като при процесите на триене се изразходва енергия, това води до намаление на общата енергия на системата. Поради това при движение на реална течност по хоризонтална тръба с постоянно сечение статичното налягане равномерно намалява по дължината на вълната. Големината на намалението зависи от дължината и сечението на тръбата и от вискозитета на течността. Колкото по-дълга и тясна е тръбата, по която се движи течността, толкова по-голямо е триенето и по-малка скоростта на изтичащата течност.

При движение на течност по тръба с променливо сечение, скоростта на течение, а оттам и статичното и динамичното налягане зависи от сечението. В места с по-малко сечение скоростта е по-голяма, а от там и динамичното налягане ще бъде по-голямо, а статичното по-малко според закона на Бернули. Тъй като течността е реална, поради вътрешното и външното триене се създава и допълнителен градиент на налягането, обратно пропорционален на сечението на тръбата.

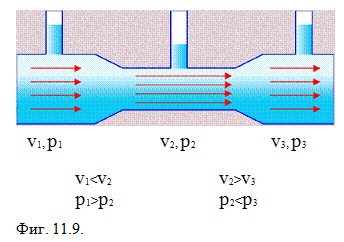
Освен това в местата на изменение на сечението в някои случаи се получават вихри, в които се губи допълнително енергия. Тези вихри са по-вероятни и по-големи при преход от по-голямо към по-малко сечение, отколкото при преход между по-малко към по-голямо сечение.

Когато сечението на тръбата се променя постепенно, налягането също се променя постепенно.

11.7. Движение на течност през последователно или успоредно свързани тръби с различно сечение

Потокът на течността, протичащ през напречното сечение на тръба за единица време можем да пресметнем от закона на Поазьой.

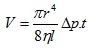
От тук потока на течността (обема течност, преминала през дадено сечение за единица време) ще бъде 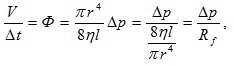където 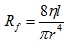се нарича хидравлично съпротивление (съпротивление при движение на флуид). По такъв начин формулата за потока на течността придобива вид, подобен на закона на Ом за електричния ток, а R_f  е аналогично на електричното съпротивление на проводник.

Нека имаме няколко последователно свързани тръби с различно сечение (Фиг. 11.11).

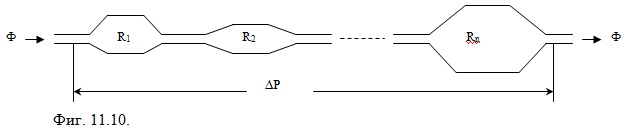
Потокът на течността през всяка от свързаните тръби ще бъди еднакъв. Следователно за ΔP можем да запишем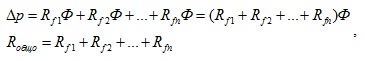

т.е. общото съпротивление ще бъде равно на сумата от хидравличните съпротивления на всяка от тръбите.

Ако имаме успоредно свързани тръби, по подобен начин можем да получим израз за общото им хидравлично съпротивление (Фиг. 11.11).

В този случай началния поток се разделя на части през отделните тръби, а разликата в налягането в краищата на тръбите е еднаква. Тогава

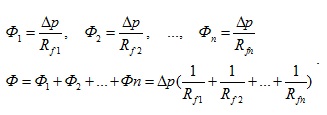
Следователно при n успоредно свързани тръби общото съпротивление е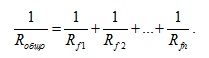

Знаейки тези уравнения, може да се пресметнат потоците на течността през различно свързани тръби, общото им съпротивление и намалението на налягането.

11.8. Движение на течност по тръби с еластични среди

При постоянно налягане и ламинарно движение на течността няма разлика в характера на движението между тръби с твърди стени и тръби с еластични стени. При променливо налягане потокът на флуида се променя (течността пулсира) и изтичащата струя от тръба с твърди стени е неравномерна. При тръби с еластични стени и достатъчна дължина изтичащата струя е непрекъсната. Под действието на повишеното налягане, създавано например от периодично действаща помпа, в тръбата за кратко време навлиза допълнителен обем течност. Това предизвиква еластична деформация (разширение) на тръбата (Фиг. 11.12). Възникналите в резултат на деформацията еластични сили изтласкват обема течност в съседен участък и т.н.

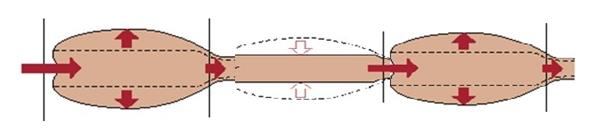
Фиг. 11.12.

В резултат на това възниква разпространяваща се по дължината на тръбата деформация, наречена пулсова вълна. Скоростта на разпространение на пулсовата вълна зависи главно от еластичните свойства на тръбата и е по-голяма от скоростта на течността.