24. Механични трептения - основни характеристики. Собствени и принудени трептения. Резонанс. Механични вълни. Биологично действие на вибрациите. Ефект на Доплер.

Трептения – това са произволни процеси, повтарящи се повече или по-малко по един и същ начин през определен период от време. В зависимост от физичната си природа те могат за бъдат механични, електрични, електромагнитни и т.н., като всички трептения се подчиняват на общи закономерности. Трептения се наблюдават навсякъде в природата – от космическите тела до живите организми. Например в звездите се извършват циклични ядрени реакции, планетите се движат периодично около Слънцето, Луната се движи периодично около Земята и това води до периодични приливи и отливи на водните басейни на Земята. Вътре във всеки жив организъм непрекъснато протичат разнообразни, ритмично повтарящи се процеси, например сърдечната дейност, хормоналните цикли, циркадни ритми и т.н.

24.1. Хармонични трептения

Механичните трептения представляват периодични движения на материални тела. Най-простият вид трептения са така наречените хармонични трептения, при които дадена величина се изменя с времето по синусов закон. Такива трептения възникват под действие на еластична сила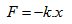

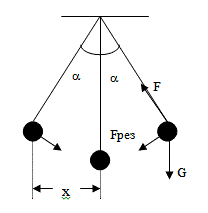
където x е отместването от равновесното положение, а k е коефициент на пропорционалност, който се нарича еластична константа. Пример за такова трептение е трептението, което извършва тяло, окачено на пружина или трептението на махало. На тялото действа сила на тежестта  G и еластична сила от страна на пружината F. В резултат на това тялото започва да трепти около някакво равновесно положение.

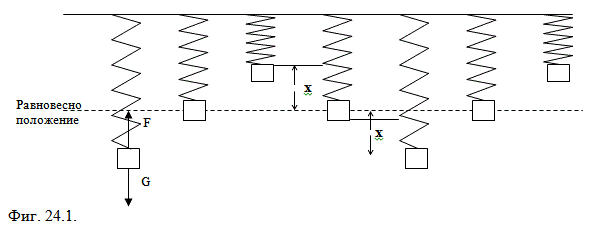
Подобно трептение извършва и едно махало (Фиг. 24.2). При махалото за мярка на отместването може да се използва или ъгълът a, или отместването x. Отместването при тези трептения може да се опише с времето чрез следната формула:

,

където А е максималното отместване, което се нарича амплитуда; 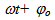е фазата на трептението; w – кръгова честота, зависеща от свойството на трептящото тяло; 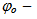началната фаза.

Фиг. 24.2.

Система, извършваща хармонично трептение, се нарича хармоничен осцилатор. Графически изменението на отместването с времето се дава със синосуида (24.3).

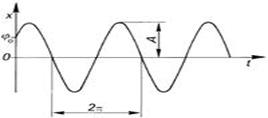
Фиг. 24.3.

Хармоничните трептения може да характеризираме с величините период Т и честота v. Период е времето, за което се извършва едно пълно трептение и следователно се измерва в секунди. Честотата на трептенията дефинираме като брой на трептенията за единица време 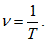. Тази величина показва колко често се повтарят трептенията и се измерва с единицата Херц [Hz]. Освен честотата се използва и величината кръгова или ъглова честота .

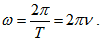От формулата за отместването може да се получат и стойностите за скоростта v и ускорението a, с които се движи трептящото тяло.

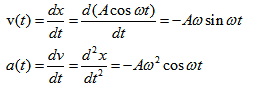
От основното уравнение на динамиката и израза за ускорението и еластичната сила може да се получи израз за кръговата честота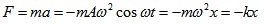

Следователно 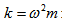и от тук можем да изразим кръговата честота w и периода на трептение Т чрез параметрите на трептящата система – маса m и еластична константа k.

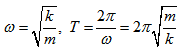
В идеалният случай, когато нямаме загуби на енергия при трептенето поради триене или съпротивление, пълната енергия Е на трептящото тяло, равна на сума от кинетичната 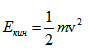 и на потенциалната му енергия 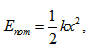, можем да докажем, че остава постоянна.

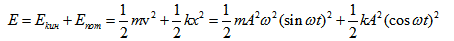
Тъй като 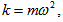, то замествайки k с неговото равно получаваме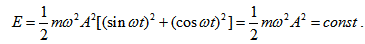

В реалните системи хармоничните трептения се съпровождат със загуби на енергия поради сили на триене и съпротивление, в резултат на което енергията на трептящото тяло намалява и с времето трептенията затихват. Амплитудата им намалява с течение на времето. Скоростта на затихване (на намаляване на амплитудата) зависи от т.н.коефициент на затихване β. Законът, по който става това намаление, се изразява с формулата 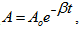, където А е амплитудата на трептенето след време t, А_о е амплитудата в началния момент t=0. Колкото е по-голям коефициентът на затихване, толкова по-бързо намалява амплитудата.

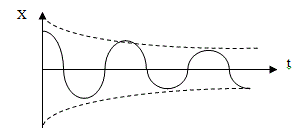
Фиг. 24.4.

На практика степента на затихване често се характеризира с величината “логаритмичен декремент на затихването λ”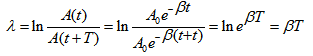

Това е величина, равна на натуралния логаритъм на отношението на две произволни амплитуди, взети през време един период.

24.2. Собствени и принудени трептения. Резонанс

Трептенията, които извършва една трептяща система (тяло), изведена от равновесното си положение, се наричат свободни или собствени. Те се извършват без участие на външна сила и честотата им зависи само от свойствата на трептящата система. Простите системи имат само една собствена честота. По-сложните могат да имат няколко собствени честоти.

В дадена система могат да възникват и трептения под действието на външна принуждаваща периодична сила. Такива трептения се наричат принудени. Те имат честота, съвпадаща с честотата на външната сила. Амплитудата на принудените трептения ще зависи от амплитудата на принуждаващата сила и по сложен начин от честотата на принуждаващата сила и собствената честота на трептене на тялото ω₀. Ако на едно тяло действа външна принуждаваща сила 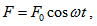, където F₀ e  амплитудата на силата, а ω - кръговата честота на принуждаващата сила, то в идеалния случай, когато няма триене, амплитудата на принудените трептения ще бъде 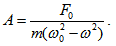. В случая, когато имаме трептения, съпроводени с триене, големината на амплитудата ще зависи и от коефициента на затихване. Тогава 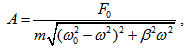, където β е коефициентът на затихване.

Следователно амплитудата на принудените трептения ще достигне максимална стойност когато ω₀=ω, т.е. когато честотата на принудените трептения съвпадне с честотата на собствените трептения на тялото. Това явление се нарича резонанс. Графически зависимостта на амплитудата на принудените трептения от честотата има вида, показан на фиг. 24.5.

 

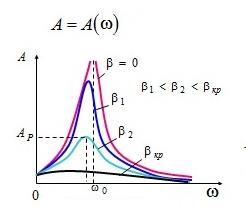
Фиг. 24.5. Зависимост на амплитудата и фазата от честотата на външната сила ω_.

Механичният резонанс може да бъде както полезен, така и вреден. Резонансът дава възможност за усилване и поддържане на трептения с малка принуждаваща сила. Същевременно той може да предизвика силно разлюляване на мостове, механични конструкции и др. тела, което може да доведе до разрушаването им.

В някои системи на трептящото тяло може да действат няколко принуждаващи сили или тялото да участва в няколко трептения. Тогава характера на резултантното трептение зависи от съотношението на началните фази, периодите, амплитудите и направленията на трептенията и в общия случай се получава някакво сложно трептение.

В практиката по-често се налага едно сложно трептение да се раздели на прости хармонични трептения. Фурие доказва, че произволна периодична функция може да бъде представена като сума от хармонични функции. Съвкупността от хармоничните трептения, които съставят едно сложно периодично трептение, се нарича негов хармоничен спектър.

24.3. Автоколебания

Съществуват системи, в които трептенията се поддържат за сметка на съществуващ в системата източник на енергия. Такива системи се наричат автоколебателни. В повечето случаи автоколебателните системи може да се представят чрез три основни елемента – трептящо тяло, източник на енергия и регулатор (Фиг. 24.6).

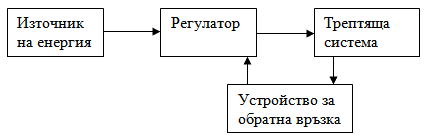
Фиг. 24.6.

Трептящата система чрез канала за обратна връзка въздейства на регулатора, като дава сигнал за състоянието на системата. Регулаторът от своя страна отваря “канал”, чрез който се предава съответната порция енергия на трептящата система. Амплитудата и честотата на автоколебателните трептения зависят само от свойствата на автоколебателната система. В това е разликата с принудените трептения, при които амплитудата и честотата зависят от външното въздействие. Класически пример за механична автоколебателна система е часовникът, в който балансът е трептящата система, пружината е източник на енергия и анкерът е регулатор за постъпването на енергия от източника в трептящата система.

Освен механични може да има и електромагнитни автоколебателни системи. Много биологични системи също са автоколебателни – например сърцето.

24.4. Механични вълни

Процесът на разпространение на трептенията, възникнали в дадена точка, в пространството около нея, се нарича вълново движение или вълна. Както трептенията, така и вълните могат за бъдат механични, електрични, електромагнитни и т.н.

 Механичните вълни са разпространяващи се в еластична среда трептения, т.е механични вълни може да имаме само във веществена среда. Механичните вълни възникват благодарение на силите на взаимодействие, които съществуват между частиците на средата. Поради това периодичните деформации, възникнали на определено място, се разпространяват в средата с някаква определена скорост.

В зависимост от посоката на трептение на частиците от средата имаме два основни вида вълни – напречни и надлъжни. При надлъжните вълни трептенията на частиците стават в направлението, в което се разпространява вълната (Фиг. 24.7). Това води до последователни сгъстявания и разреждания на веществото при преминаване през него на напречна вълна. Надлъжни вълни възникват в твърди, течни и газообразни среди.

Фиг. 24. 7.

При напречните вълни частичките трептят в направление, което е перпендикулярно на посоката, в която се разпространява вълната (Фиг. 24.8). Напречни вълни могат да възникват само в твърди тела.

Скоростта на разпространение на вълните зависи от плътността и от еластичните свойства на средата.

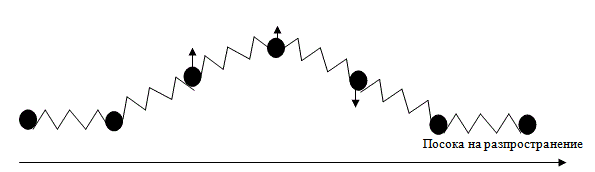
Фиг. 24.8.

Вълновият процес се описва чрез величините, които характеризират трептението, предизвикало вълните – период Т, кръгова честота 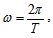, амплитуда А. Друга характеристика на вълната е величината дължина на вълната λ. Това е разстоянието, на което се разпространява трептението за време, равно на един период, т.е. разстоянието между две най-близки точки, които трептят с еднаква фаза (Фиг. 24.9).

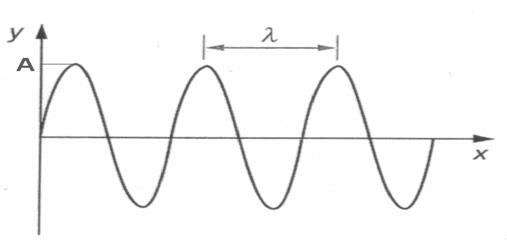
Фиг. 24.9.

Следователно 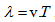, където v е скоростта, с която се разпространява вълната. Друга величина, с която характеризираме вълните е “фронт на вълната” – това е повърхността, до която едновременно достига вълновият процес от един източник на трептение. Друга дефиниция е множеството от точки, които трептят едновременно с еднаква фаза. Формата му фронта на вълната зависи от формата на източника, от свойствата на средата, в която се разпространява вълната и от разстоянието до източника.

Нека вълна се разпространява по остта ОХ без затихване, така че амплитудата и във всички точки остава еднаква (Фиг. 24.10). Източникът на трептение се намира в точка с координати х=0 и той трепти хармонично, т.е. отместването s на източника на трептения с времето се дава с уравнението .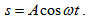

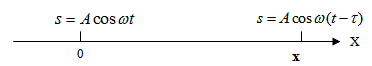
Фиг. 24. 10.

До точка с координата х трептенията достигат със закъснение след някакво време t. Следователно трептенията в точка х можем да опишем с уравнението 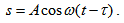 . Времето t можем да изразим чрез разстоянието х и скоростта на разпространение на вълната 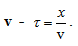. Тогава уравнението на вълната в произволна точка от средата, която се намира на разтояние х от началната точка ше бъде 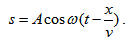. Тази формула може да се преобразува като въведем една нова променлива – вълново число 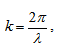, където λ е дължината на вълната. Тогава уравнението на вълната ще има вида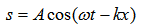

Разпространението на вълната е свързано с пренасяне на енергия. Количествена характеристика на пренесената енергия е величината поток на енергията Ф. Тя се дефинира като енергията Е, пренесена за единица време през дадена повърхност S, която е перпендикулярна на посоката на разпространение на вълната, следователно 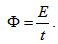. Единицата за поток на енергията е ват (W).

Потокът на енергията, пренесен от вълната за единица време през единица площ, перпендикулярна на посоката на разпространение на вълната, се нарича плътност на потока на енергията или интензитет на вълната 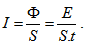. Единицата за интензитет е W/m². Ако източникът на вълната е точков и е с постоянна мощност, то интензитета ще бъде пропорционален на реципрочната стойност на квадрата на разстоянието r от източника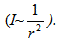  

Имайки предвид, че енергията на трептящо тяло е 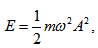, и приемайки, че в единица обем се намират n частици, то специфичната енергия на трептенето на средата (енергията на единица обем), ще бъде .

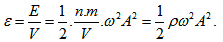Тогава интензитетът на вълната можем да изразим чрез специфичната енергия на трептене.

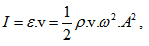, където е v е скоростта на разпространение на вълната, а ρ е плътността на средата. Следователно интензитeта на вълната е пропорционалeн на плътността на средата, скоростта на разпространението, квадрата на кръговата честота и на амплитудата на трептенията.

24.5. Биологично действие на вибрациите

В техниката под вибрации се разбират механични трептения на различни конструкции и машини. Те могат да окажат влияние на човек или животно при допир до вибриращите предмети. Механизмът на действието им е свързан с възникване на принудени трептения на вътрешните им органи, резонансно разлюляване на органи или отделни части от тях, възникването на променливи ускорения и др.

Тяхното действие може да бъде както полезно, така и вредно. Например трептящи тела се използват за различни видове вибромасаж. Същевременно продължително излагане на действието на вибрации (например продължителен  контакг на миньори с пробиващи инструменти, шофьори при каране на камиони и автобуси и т.н. ) може да доведе до възникването на вибрационна болест, която е една от най-тежките професионални болести.

24.6. Ефект на Доплер

Ефект на Доплер се нарича изменението на честотата на вълната, приемана от наблюдател (приемник на вълните), при относителното движение на източника на вълната и наблюдателя.  

Нека имаме наблюдател, който се приближава със скорост v_н до неподвижен спрямо средата източник на вълна с честота ν₀ и скорост на разпространение v (Фиг. 24.11).

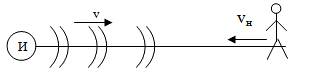
Фиг. 24.11.

Тогава честотата на вълната, възприемана от наблюдателя, ще бъде 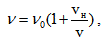, или наблюдателят ще възприема вълната с по-голяма честота. Ако пък наблюдателят се отдалечава от източника, тогава формулата ще има вида 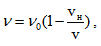, т.е. вълната ще се възприема от наблюдателя с по-малка честота. Двете формули можем да обединим в обща формула 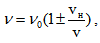, като знакът + се отнася за приближаващ се до източника наблюдател, а знакът – за отдалечаващ се наблюдател.

Подобен ефект ще се наблюдава и в случая, когато източникът се движи спрямо наблюдателя със скорост v_и. Тогава честотата на вълната, която достига до наблюдателя ще бъде 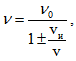, като тук знакът + се отнася за отдалечаващ се източник, а знакът – за приближаващ се източник. Ефектът на Доплер може да се наблюдава например когато пътник се намира на перона на гара. Когато влак се приближава или отдалечава от пътника, се наблюдава промяна в честотата на сирената на влака.

Възможен е и случай, когато едновременно се движат и наблюдателя, и източника, като те се приближават или отдалечават един към друг (Фиг. 24.12).

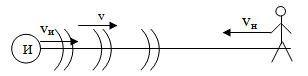
Фиг. 24.12.

Тогава честотата, която ще се възприеме от наблюдателя ще бъде 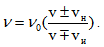. Горните знаци се отнасят за случая, когато източника и наблюдателя се приближават, а долните когато се отдалечават. От формулата се вижда, че когато източникът и наблюдателят се движат с еднакви по големина и посока скорости, няма да се наблюдава промяна в честотата на регистрираната вълна.

Важно приложение в медицинската диагностика има случая, когато генератора на вълните и приемника се намират в едно устройство, а възниква отражение от движеща се повърхност (Фиг. 24.13).

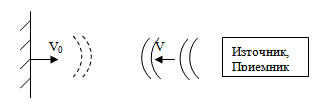
Фиг. 24.13.

Нека генераторът излъчва вълна с честота ν₀ и скорост на разпространение v, а скоростта на движещата се повърхност е v₀. Повърхността първо можем да я считаме като движещ се приемник на вълната, а след това като движещ се излъчвател. Имайки впредвид формулите за движещ се приемник и излъчвател, може да се изчисли честотата, възприемана от приемника 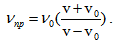. От тук можем да пресметнем разликата между честотата на генератора на вълните и честотата, регистрирана от приемника, която се нарича Доплеровско отместване ν_Д.

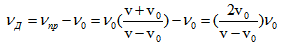
Ако скоростта на движение на движещата се повърхност е много по-малка от скоростта на разпространение на вълната (v>>v_o), както е в случая с медицинските изследвания, при които ултразвукови вълни се отразяват от клапите на сърцето или стените на сърцето, то можем да пренебрегнем v_o  в числителя и да получим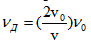

За възникване на ефект на Доплер не е задължително вълната да се отразява от плътна движеща се повърхност. Такъв ефект може да възникне и при отражение от частици, движещи се в поток от течност, както са кръвните клетки в кръвта.