Методика на педагогическите изследвания за студенти и учители

ТЕМА № 3.

СТАТИСТИЧЕСКИ АНАЛИЗ НА РЕЗУЛТАТИТЕ ОТ ПЕДАГОГИЧЕСКО ИЗСЛЕДВАНЕ.

При педагогическите изследвания се прилага различен комплекс от изследователски методи. Част от тях служат да се установи връзката между определени мерки с характеристиките на обектите за изследване. Тази връзка се установява, представя и обосновава чрез математико-статистически методи.  При тях се оперира с числените, а не с действителните значения на даден признак. Всеки метод може да се приложи към дадена съвкупност от числа, разбира се, с известни ограничения. Особеностите на различните методи следва да се познават и да се използват оптимално. В концептуалната част на изследването математико-статистическите методи се описват в методическата част, като включват процедурите по: формиране на извадка и образуване на групи; определяне на променливата (променливите) и критериите и показателите на изследването, разработка на модел за анализ на данните.

3.1. ОСНОВНИ ПОНЯТИЯ. ЕТАПИ НА СТАТИСТИЧЕСКИЯ АНАЛИЗ.

Използването на статистическите методи се основава на определени изисквания. Разработени са различни методи и техники за анализ на резултати от педагогически изследвания, чрез които се сравняват установените данни, определя се степента на надеждността им, установяват се отношения между числовите стойности и техните зависимости, доказват се хипотезите на изследването, аргументират се изводите, до които достига изследователя. В това се изразява и задачата на статистическия анализ. Но, универсални методи за анализ не са разработени и не всеки метод е подходящ за всяка съвкупност от данни. Различните методи за анализ се прилагат към определени ситуации. За да изберем подходящия анализ, при всяко конкретно изследване е необходимо да се съобразим с:

• обема на извадката;
• използваната оценъчна скала;
• вида на разпределение на променливата;
• броят на променливите, които се наблюдават и измерват;
• поставената цел и вида на хипотезата и др.

Прилагането на статистическите методи изисква представяне на установените резултати в подходяща форма за математическа обработка и анализ – таблична и графична. Следва изчисляване на определени величини – #средни величини# и #величини на разсейване#. Изчислените величини се използват при различните видове статистически анализи, съобразно поставената цел на изследването, за разкриване на връзки и закономерности в изучаваните явления (21).

Тази част от изследователската работа условно може да се раздели на три етапа:

• Структуриране и подреждане на първичната количествена информация във форма, подходяща за по-нататъшна обработка.
• Систематизиране, обобщаване и групиране на количествените данни и представянето им в таблична и графична форма и чрез статистически величини.
• Статистически анализ на данните и разкриване на връзки и закономерности в изследваните обекти, в съответствие с приложените педагогически въздействия.

Първите два етапа се означават общо като представяща статистика, а третия - доказателствената статистика. Статистическият анализ има за цел потвърждаването или отхвърлянето на формулираната хипотеза на изследването. Чрез него се установяват:

• качествата на разработените методи и средства (диагностика на методи и средства);
• статистическата значимост на получените резултати от проведено емпирично изследване (проверка на статистически хипотези);
• закономерността или случайността на регистрираните емпирични резултати;
• извеждат се причинно следствени връзки и закономерности (Фиг. 30).

 

 

 

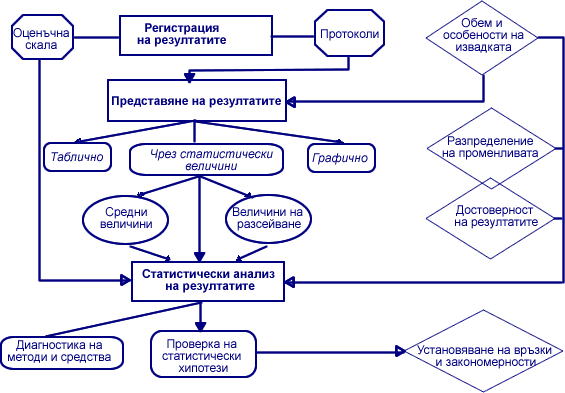
Фиг. 30. Представяне и анализ на емпирични резултати.

Авторите съзнават, че в тази част на учебника ще се сблъскате с много непознати понятия. С подходящи примери ще разкрием съдържанието на тези понятия, както и на процедурите, свързани с анализа на изведени резултати от конкретно изследване. В началото ще се върнем отново към понятието извадка, ще разкрием същността на оценъчните скали и последователно ще преминем през етапите на представянето на резултатите. В края на тази част с примери ще илюстрираме процедурите на приложението на някои по-характерни методи за статистически анализ на установени резултати от педагогическо изследване.

3.1.1. ОБЕМ  И ОСОБЕНОСТИ НА ИЗВАДКАТА.

Обикновено, при едно педагогическо изследване не е необходимо да се обхванат всички изследвани лица. Формирането на извадка като част от генералната съвкупност облекчава организацията на изследването, но за да бъде тя представителна е необходимо да се спазват определени изисквания. Преди всичко, елементите на извадката трябва да отразяват най-общите и типични качества на генералната съвкупност.

При предварителното планиране на едно изследване трябва да се съблюдават следните положения:

А. Колко голяма (с какъв обем)трябва да бъде извадката?

Б. От каква гледна точка може и трябва да се обобщи?

В. Може ли да се използва контролна група?

А. По отношение на необходимия обем на извадката не могат да се дадат задължителни указания. За изследване на един малко разсейващ се белег е достатъчна относително малка извадка. При белези, които се изменят много, е необходима по-голяма група. За да се обяснят значителни разлики между две групи, са достатъчни малки извадки; колкото по-незначителни са разликите, толкова по-големи трябва да бъдат извадките, за да може да се докаже значимостта на разликата.

В статистиката една извадка се приема за „голяма”, щом като тя обхваща повече от 30 елемента. Всички извадки при n<30 се означават като „малки”.  Разпределението на числовите характеристики при големи извадки се доближава все повече до нормалното; напротив разпределенията от малки извадки се подчиняват на разпределение t. Следователно безусловна предпоставка за приложение на модела на нормалното разпределение при статистически заключения  е  големината  на  извадката п>30.  За оценка на характеристики от малки извадки не трябва да се използва нормално разпределение; от друга страна обаче, разпределението t може да се приложи при извадки с голям обем n. Общо взето, минималната извадка не бива да е по-малко от 10—15 лица. Най-често броят на изследваните лица трябва да бъде между 30 и 100. Изследователят съобразява, според особеностите на своята проблематика, дали за постигане на поставените цели е необходима голяма извадка или малка, но основно изследвана.

Б. Подборът на лицата за изследване трябва да се осъществи така, че да се получи случайна извадка. Изследователят трябва да бъде наясно коя генерална съвкупност ще характеризира с получения резултат. Затова той трябва да се погрижи подборът на индивидите, принадлежащи към тази съвкупност, да не  става според каквито и да е субективни преценки, а случайно.

В. При изследвания, имащи за цел проверката на една хипотеза, се препоръчва да се състави план, включващ използването на контролни групи. По този начин се улеснява много получаването на точни и убедителни изводи. Обикновено се постъпва по следния начин: определят се две еднакви извадки “А” и “В”. Двете се подлагат на изследване при строго определени условия. Получените при това изменения се регистрират и анализират. Много по-целесъобразно е да се сравнява една контролна група с повече експериментални групи, при което всяка една от последните представя отделни вариации на експерименталните условия. Тук следва да се посочи една особеност: щом искаме да интерпретираме получените разлики между числовите характеристики от контролната и експерименталната група, тези групи трябва да се подложат на влияния, които са сравними (32).

В някои случаи е възможно в процеса на изследването да се разменят условията, при които работят експерименталните и контролните групи. Този метод се нарича инверсия. Той е препоръчителен, като по този начин значително се повишава показателната сила на резултатите.

3.1.2. ОЦЕНЪЧНИ СКАЛИ (СКАЛИ ЗА ИЗМЕРВАНЕ)

За представяне на резултатите чрез някой от начините на представящата статистика е необходимо предварително да се кодират количествено. Това се осъществява посредством избрана скала за измерване. За педагогическите изследвания са подходящи следните скали: номинална, рангова и интервална.

Номинална скала се ползва, когато извадката може да се разбие по определени признаци на непресичащи се класове, в случаите когато се отчита наличие или отсъствие на определен признак на наблюдавания обект.

Пример. На поставените въпроси в анкетата може да се отговори с Да, Частично и Не, а може и да не се даде отговор. Установените резултати се фиксират в таблица.

Таблица 1.

Цифрите в последния ред са елементи на #номинална скала#. Тя е подходяща, когато като метод на изследване се използва анкета. Същественото е, че с тези числа не се извършват никакви действия, а се използват количествата, които показват принадлежност на елементи от извадката към съответен клас.

#Рангова скала# се използва, когато това, което се оценява се състои от неравностойни съставки, т.е. задачите са с различна трудност, сериите от въпроси са неравностойни, изпълнението на определени практически дейности изисква различна степен на формираност на  умения и т.н. В тези случаи различните по трудност съставки се оценяват с различни числа. Такава е общоприетата в България схема за оценяване на учениковите постижения – 2, 3, 4, 5, 6.

Например:

Ако заданието се състои от седем въпроса, подредени по трудност (във възходящ ред), то оценяването на отговорите можем да осъществим чрез рангова скала така:

Таблица 2.

Ако на някой от  въпросите не е отговорено, то оценката е 0 точки.

Получената поредица 0, 1, 3, 4, 6, 9, 12 е рангова скала.

#Интервална скала# се използва, когато задачата е съставена от равностойни съставки. Ако е отговорено на 6 въпроса се приписват 6 точки, на 4 – 4 точки и т.н. Получава се редицата: 6, 5, 4, 3, 2, 1, 0, която представлява интервална скала (21, 32).

3.2. ПРЕДСТАВЯНЕ НА РЕЗУЛТАТИТЕ ОТ ПЕДАГОГИЧЕСКО ИЗСЛЕДВАНЕ (ПРЕДСТАВИТЕЛНА СТАТИСТИКА).

За да се направи добър количествен анализ е необходимо резултатите от изследването да се представят в подходяща за обработка форма, като се използват най-често срещаните способи: табличен, графичен и чрез статистически величини.

3.2.1. ТАБЛИЧНО ПРЕДСТАВЯНЕ НА РЕЗУЛТАТИТЕ.

Таблицата е една от най-рационалните форми на представяне на резултати от проведено педагогическо изследване чрез целенасоченото им групиране. Тя дава визуална представа за връзките между данните, предназначени за количествена обработка. 

Таблицата представлява комбинация от хоризонтални редове и вертикални колони, които задължително се именуват. В колоните и редовете се фиксират числовите стойности на показателите, характеризиращи променливата на изследването.

Първият ред на таблицата (антетка) показва смисъла на съдържащите се в колоните данни.

Първата колона предава съдържанието на редовете. Тя включва списък на групираните данни.

Наименованието на таблицата съдържа в кратка и синтетична форма основната й качествена характеристика.

Таблицата без числени стойности само с антетката и означено съдържание в първата колона представлява макет на тази таблична форма.

За да се подложат на статистически анализ резултатите от едно конкретно изследване, е необходимо те да се представят по подходящ начин. Тази дейност е свързана с първоначално фиксиране и следваща последователна обработка - систематизиране, групиране и обобщаване на данните. Тя се определя като подготовка на данните за анализ и включва:

1. фиксиране на данните в подходяща форма – изготвяне на протокол;
2. обобщаване на крайните резултати за всяко от изследваните лица;
3. ранжиране на резултатите – построяване на “рангов ред”;
4. извеждане на вариационен ред;
5. групиране на данните. Определяне на честотните им характеристики;
6. представяне на данните чрез честотна таблица.

Ще проследим всеки от тези етапи на подготовката на данните за анализ и представянето им в таблична форма чрез конкретни примери.

Първи етап. Фиксиране на изведените данните в подходяща таблична форма. 

Изготвяне на #първичен протокол#.

След като е избрана скалата, резултатите се кодират и се изгражда протокол. Той представлява разгърнат списък на елементите от извадката (изследваните ученици) и отделните оценки по задачите. Протоколите се оформят най-често в таблична форма и се представят обикновено в приложение на разработката. Използват се различни начини (варианти) за подреждане на резултатите в таблици, като се съобразяват и с използваната оценъчна скала.

Таблица 3. Първичен протокол  (при номинална скала)

Таблица 4. Първичен протокол  (при тестова форма)

Какви са особеностите на първичния протокол при представяне на резултатите от тест и каква информация можем да извлечем от него?

На първо място, с получер шрифт под всеки въпрос са маркирани верните отговори на задачите от теста. Въпрос 4 е със свободен отговор и при попълването на тази колона се отчита само дали отговорът е верен или не.

Последният ред представя сумите в съответните колони. При въпросите със структуриран отговор тази информация ще ни послужи за анализа на работата на дистракторите.

Последните четири колони представят информация за това, кои задачи са решавани или пропуснати от тестираните, и индивидуалните им резултати „колони „Вярно“ и „Грешно“). Сумите в клетките на последните четири колони се използват при някои анализи на качествата на диагностичното средство (Тест на Хойт).

Таблица 5. Първичен протокол  (при интервална скала)

Сумите в последния ред представят резултатите по задачи, а в последната колона – индивидуалните резултати.

Втори етап. Обобщаване на крайните резултати за всяко от изследваните лица.

Преди да се пристъпи към анализ на получените резултати, необходимо е те да се представят в по-обобщен вид. За тази цел първоначално от изготвения протокол се прави списък на крайните резултатите на всяко от изследваните лица.

Пример:

Проведен е дидактически тест с 20 ученика. Изготвен е списък на крайните резултатите на учениците по азбучен ред според номерата им в дневника. Максималната оценка - бал, която може да получи ученик, справил се безгрешно с въпросите е 45 точки.

Таблица 6. Обобщени крайни резултати за изследваните лица

Този списък е необходим етап от подготовката на резултатите но недостатъчен, тъй като не позволява да се направят обобщени изводи. Така, за ученика с пореден номер 18 знаем, че е получил бал 32 точки, но не знаем на кое място в класацията го поставя този резултат.

Трети етап. Ранжиране на резултатите. Рангов ред.

 Това изисква, да се подредят резултатите в низходящ ред, започвайки от максималният постигнат резултат. Ето данните на тридесет изследвани ученика, подредени по рангове.

Пример:

Таблица 7. Рангов ред на резултатите на изследваните лица

Ранговото подреждане дава отговор на въпроса по отношение класирането на резултатите. Така, ученикът с пореден номер в класа 10 има пети ранг от всичко дванадесет, т.е., среден резултат.

Представянето на резултатите по този начин не изключва индивидуалните особености на всеки елемент от извадката. Когато анализира резултатите, изследователят неминуемо ще се ръководи от индивидуалните качества на всеки ученик. За да се избегне това, като се има предвид, че статистиката работи със статистически единици, а не с индивидуалности, се преминава към следващия етап (28).

Четвърти етап. Извеждане на #вариационен ред#.

Ако подредим числата xi, които са оценки на някакво качество (променлива величина) на елементите от извадка с обем n, като на първо място поставим най-малкото число, след това следващото и т.н. се получава така наречения вариационен ред. В разглеждания пример (Табл. 7) редът ще бъде x₁=29, x₂=30, x₃=31, x₄=32, ..., x₁₇=45.  Вариационният ред не може да се определи предварително. Той се изгражда от установените за конкретното изследване резултати. Първият елемент на вариационния ред е най-ниската фиксирана стойност на променливата, а последният  е най- високата стойност.

На практика често се случва за някоя от стойностите на вариационния ред да няма фиксиран резултат на променливата. Така в използвания пример за стойността х=44, няма установен резултат от изследването. Но при други стойности на елементите на вариационния ред са установени повече от един резултати.

Пети етап. Групиране на данните. Определяне на честотните им характеристики. Представяне на данните чрез честотна таблица.

За педагогическите изследвания има значение определянето на абсолютната, относителната и натрупаната честота. Всяка от тях съдържа информация, необходима за сравняване и извеждане на връзки и закономерности в изследвания обект.

Честотните характеристики са необходими и за определянето на статистическите величини. Практически удобно се оказва конструирането на т.н. честотна таблица. В първата й колона се отразяват елементите на вариационния ред във възходящ ред. Във втората колони се нанасят стойностите на абсолютната честота, в третата - на натрупаната честота, а в четвъртата – на относителната честота. По този начин се достига до още по-прегледна и информативна таблица, в резултат на което се получава честотно разпределение на променливата.

Таблица 8. Честотна таблица № 1

#Абсолютна честота# - f_i

Абсолютната честота е числото, което показва колко пъти се среща дадена оценка хi в извадката.

В примера - резултат от 42 точки се среща един път, следователно честотата му е числото 1. Абсолютната честота на резултата 41 точки е числото 5 и т.н.

#Натрупана честота# - F_i

Натрупаната честота е числото, което показва колко елемента от извадката имат резултат по-малък или равен на резултата на съответен елемент. От определението се вижда, че

F_i =f₁+f₂+f₃+ ... +f_i

Така, натрупаната честота F₄₃= 28 (ред 15 от таблицата) показва, че 28 ученици имат 43 и по-малко точки от проведеният тест.

#Относителна честота# - f_{i отн.}

Това е числото, показващо каква част от елементите на извадката имат резултати, равни на тези на елемента x_i, т.е.:

Формула 3 

Тази честотна характеристика е необходима и се използва при сравняване на резултати, установени при две извадки с различен обем.

Какво показва например f₁₃ = 5/30? Тази характеристика ни дава основание да твърдим, че една шеста  (5/30 = 1/6) от всички ученици имат резултат 41 точки.

3.2.2. КЛАСИФИЦИРАНЕ НА ДАННИТЕ.

Честотната таблица не е достатъчно прегледна, когато съдържа много величини (дълъг вариационен ред). В този случай е по-добре да се намали броя на данните, като се обобщават две или повече съседни стойности в един клас. Чрез такова групиране се постига по-голяма яснота и нагледност.

Преди да се представи техниката за образуване на класове, ще се наложи дефинирането на няколко понятия.

#Класът#

Границите на даден клас (интервалните граници) се образуват от най-малката и най-голямата величина на този клас.

#Средата на класа# е средната аритметична от двете граници на класа. Най-често тя служи за означаване на класа.

#Ширината на класа# (областта на класа) при дискретните променливи е броят на обхванатите величини в класа. Той се получава от разликата на две последователни средни величини и се означава с h (h>0).

Отворени класове са тези, в които са обхванати величини над или под определена граница.

Например: При променливата „възраст на изследваното лице” отворени класове са „под 18 години” или „над 65 години”; при класовете “повече от 6 мнения” или „по-малко от 2 грешки” се касае също така за отворени класове.

При групиране на данните трябва да се избере най-удобната ширина на класовете и най-целесъобразното им начало.

Как се извършва избора на ширината на класовете ?

Ако класовете са с голяма ширина те са относително малко. Колкото по-малка е ширината на класовете, толкова е по-голям техният брой. Ако се избере съвсем малка ширина, тогава таблицата става много подробна и случайните влияния се отразяват неравномерно. Ако се избере много голяма ширина на класовете, някои особености на разпределението се заличават, въпреки че са съществени за проблема. Следователно, важно е да се намери такава оптимална ширина на класовете, която способства за получаване на информация при минимум класове. При избор на ширината на класовете не могат да се дадат задължителни указания. Следните препоръки биха могли да бъдат полезни при отделните случаи:

- Броят на класовете обикновено трябва да е между 10 и 20.

- Ширината на класовете трябва да бъде по възможност нечетно число. Това е по-удобно при следващите изчисления, тъй като тогава средата на класа xk ще бъде цяло число.

Броят на   класовете се определя от формулата:

формула 4             K = 1 + 3. lg n

където:  К - брой на интервалите, определящи класовете,

n - обем на извадката.

Таблица 9 съдържа стойностите на К в различни диапазони на n.

Таблица 9. Стойности на коефициента К:

Интервалите, които покриват класовете трябва да имат еднаква ширина. Определянето й става по следния начин:

формула 5

където:

h - дължина на всеки от интервалите;

x _max. - най- висок резултат;

x _min - най- нисък резултат;

K - намереният таблично или изчислен брой на класовете.

Например:  Понеже извадката, съгласно таблица 7 е от 30 елемента, то обемът й е в диапазона 23 - 46, т.е. К = 6

Обикновено полученото число е десетична дроб, която се закръгля по подходящ начин. Добре е първият клас да съдържа число, което е по-малко от най-ниския резултат в извадката. В примера, класовете изглеждат така:

Таблица 10. Абсолютна честота по класове

3.2.3. ГРАФИЧНО ПРЕДСТАВЯНЕ НА РЕЗУЛТАТИТЕ

Графичното представяне на резултатите от педагогическите изследвания е важно допълнение към статистическия анализ. То е ефективно средство за демонстрация на резултатите и визуализиране на зависимостите. За тази цел се използват различни графични форми: хистограма, полигон, кръгова диаграма, стълбчеста диаграма и др.

При #хистограмата# честотата на всяка величина (или всеки клас от величини) се изобразява чрез повърхнината на правоъгълник, който се получава от тази величина (или клас). Поради формата си хистограмата се означава също така и като стъпаловиден полигон.

Разглежданата досега таблица на честотата можем да приемем като таблица от стойности, в която на всяка величина Х отговаря нейната честота f_j. В първия квадрант на една правоъгълна координатна система нанасяме на абсцисата величината X_i и върху ординатната ос - честотата f_j. Разпределението на честотата се представя като хистограма, в която са начертани правоъгълници, чиито основи са измерените величини, а височините им са техните честоти. При това трябва да се има пред вид, че честотата f е безразмерна величина, докато величината х е именувана, чиято мерна  единица  (напр.  см.,  гр., сек., точки) винаги трябва да се посочва.

#Полигон# се нарича начупената линия, която съединява точки с координати (xi, fi). На абсцисата (х) се нанасят съответните оценки (xi) или средата на оценъчния интервал на съответните оценъчни категории, а на ординатата (fi) се нанасят стойностите на  абсолютната (или на относителната) честота.

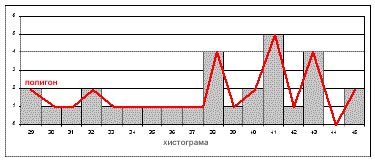
Фиг. 31. Хистограма и полигон.

Представянето с #кръгова диаграма# (или още секторно представяне) е удобно преди всичко за изобразяване на процентни честоти, като цялото лице на кръга отговаря на 100%. Отделните сектори получават големини, съответстващи на представената част. Централните ъгли a за всеки сектор се изчисляват, както следва: 

a = f. 3,6°

Централните ъгли се нанасят с ъгломер. Отделните сектори на честотата изпъкват по-ясно, ако се оцветят различно или защриховат. При повече категории и тази форма става непрегледна. На кръговата диаграма са представени данните от таблица 10 – резултатите от тест като класифицирани величини.

 

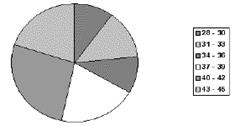
Фиг. 32. Кръгова диаграма.

#Стълбчестата диаграма# показва чрез лицата на правоъгълници как се отличава честотата на белезите в качествено различни извадки.

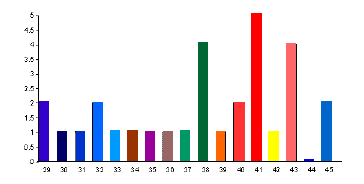
Фиг. 33. Стълбчеста диаграма.

Стълбчестата диаграма изглежда идентична с хистограмата. Двете форми на представяне се различават една от друга по следните показатели:

1. Линията,  върху  която  са  издигнати   колонките   на  стълбчестата диаграма, не съдържа измерени величини, а номинални   класове  от качествено различни   променливи.

2. Мястото на оста на честотата в равнината е произволно. Често тя е вертикална, много често обаче лежи също така и хоризонтално  (както на фиг. 30. а).

3. Колоните имат различна ширина, без обаче да граничат непосредствено   помежду си, а са разделени от дистанции с произволна дължина.

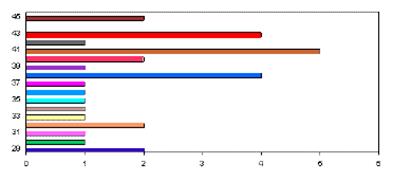
Фиг. 33.а. Стълбчеста диаграма.

 

3.2.4. ПРЕДСТАВЯНЕ НА РЕЗУЛТАТИТЕ ОТ ИЗСЛЕДВАНЕТО  ЧРЕЗ СТАТИСТИЧЕСКИ ВЕЛИЧИНИ.

Статистическият анализ на резултатите от едно педагогическо изследване се основава на описанието на разпределението. За да се достигне до обобщено описание на разпределението се определят основните му статистически числови характеристики –средни величини и величини на разсейване. Средните величини са числови характеристики, с които се означава разпределението върху числовата ос, а величините на разсейването характеризират ширината на разпределението.

3.2.4.1. СРЕДНИ ВЕЛИЧИНИ.

#Средноаритметична на вариационния ред# - ().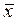

Получаването на тази величина е твърде леко и при едно нормално разпределение тя е добра характеристика за състоянието на извадката.

формула 6

където:

x_min - най-нисък резултат

x_max - най-висок резултат

В примера:

Това показва, че средният резултат на извадката е числото 37.

#Средноаритметична на разпределението# - (x_i)

Формула 7

За определянето й e необходимо честотната таблица да бъде допълнена с още една колона (x_i.f_i):

Таблица 11. Честотна таблица № 2

За примера:

Тази величина е различна от величината на средната аритметична на вариационния ред и още по-добре характеризира състоянието на конкретната извадка, а оттам - и на генералната съвкупност.

#Мода на разпределението# – (m)

Тази величина е добра характеристика на състоянието, когато разпределението е едно - модално или най-много двумодално. В случай на едномодално разпределение модата е m= x_i (max. f), т.е. величината с най-голяма честота. Тя се определя предимно при извадки с голям обем, за изучаване на качествени признаци и при разпределния с много върхове.

В примера m = 41, тъй като най-голям брой ученици (5) имат тази оценка.

#Медиана# - (Z)

Медианата Z е онази  стойност, която разполовява ранговия  ред, получен от подредените по големина измерени величини.

При нечетно число Х медианата е една от измерените величини на реда.

При четно число Х медианата лежи между числата в средата на реда, като е средноаритметична от тях.

3.2.4.2. ВЕЛИЧИНИ НА РАЗСЕЙВАНЕ

Тези величини характеризират степента на еднородност на съвкупността от данни и границите на вариация на променливата.

 #Дисперсия# - (S_x²)

Като величина на разсейване, дисперсията показва в какъв диапазон е нормално да се отклоняват отделните величини (резултати) от средната стойност.

За определяне на тази величина има практическо правило. За целта допълваме честотната таблица с още три колони (6-та, 7-ма, 8-ма колонки).

Таблица 12. Честотна таблица № 3

Дисперсията се изчислява по формулата:

формула 8

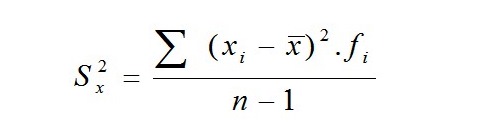
В примера:

 

Обикновено дисперсията се получава като десетична дроб, която по подходящ начин се закръгля до цяло число.

В посочения пример, диапазонът в който е нормално да се отклоняват величините (допустим интервал на вариационният ред) е интервала:

формула 9

#Средно квадратично отклонение# - (S_x)

Чрез средно квадратичното отклонение се определя интервала на статистическа достоверност (T_Д):

формула 10

И в този случай е необходимо получената стойност да се закръгли до цяло число, т.е. стойността на Sx е 5.

формула 11

T_Д: [xi - Sx ; xi + Sx]

За примера:

T_Д: [38-5;8+5] = [33 ; 42]

В такъв случай се налага преизчисляване на представителните статистически величини: средно аритметично на вариационния ред, модата и средно аритметичната на разпределението.

За примера, те са съответно:

Средно аритметично на реда:

Мода: m = 41; (f₄₁=5)

Средно аритметична на разпределението:

Сравняването на стойностите на получените величини показва:

|x<x_i<m|,

което позволява да се твърди, че съответното задание е твърде леко за учениците от извадката.

Коефициент на вариация (V)

Тази величина служи за сравняване на разсейванията при различни по големина х    

Формула 12

 

3.2.5. ЧИСЛОВО РАЗПРЕДЕЛЕНИЕ. ФОРМИ НА РАЗПРЕДЕЛЕНИЕ.

В статистиката съществува обща тенденция за свеждане на наблюдаваните закономерности на случайното разсейване към кривата на нормалното разпределение. Разпределението на променливата в една съвкупност е нормално, когато е резултат от едновременното въздействие на многообразни фактори и влиянието на всеки поотделно е нищожно малко в сравнение с влиянието им като съвкупност. Това разпределение има симетрична камбановидна форма и носи наименованието крива на Гаус - Лаплас, по-известно като гаусова крива (гаусово разпределение).

 

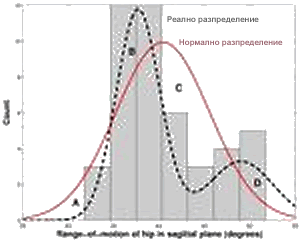
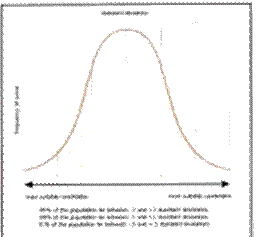
Фиг. 34. Гаусова крива.

Изведен е закон за нормалното разпределение: в нормалното разпределение вероятността отделните величини да са в определените от х_i и S граници е: 68 % за х_i+S; 95 % за х_i+2S; 99,7 % за х_i+3S. Този закон е известен още като правило за трите сигми. Според него, ако в едно разпределение 99,7 % от отделните значения на променливата лежат в диапазона х_i+3S, то разпределението й е нормално.

При графичното изразяване едно разпределение може да има различна форма. Известни са типични форми на разпределения, с определени особености, които дават важна информация за изследвания обект.

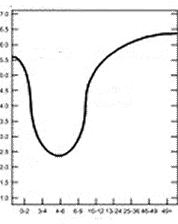
Фиг. 35. U – образно разпределение. Това разпределение показва че граничните величини се срещат много по-често от средните

 

Фиг. 36. Семейство на нормалните криви

Фиг. 37. Едномодално разпределение

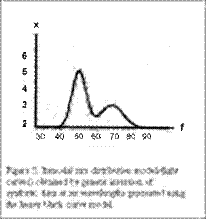
Фиг. 38. Бимодално разпределение

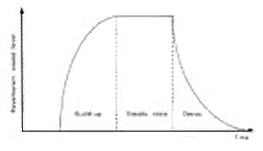
Фиг. 39.  Безмодално разпределение

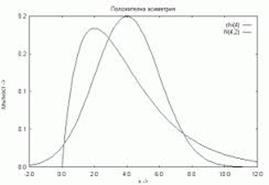
Фиг. 40. Разпределение с отрицателна асиметрия

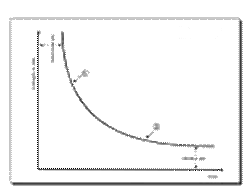
Фиг. 41. Разпределение с положителна асиметрия

До тук описахме първите два етапа от анализа на установените резултати, означени общо като представяща статистика. Третият етап – доказателствената статистика, има за цел потвърждаването ли отхвърлянето формулираната хипотеза на изследването.

В следващата част се разкрива съдържанието на доказателствената статистика и се илюстрират процедурите по приложението на някои по-характерни методи за статистически анали на установени резултати от педагогическо изследване.

 

 

 

3.3. СТАТИСТИЧЕСКИ АНАЛИЗ НА РЕЗУЛТАТИ ОТ ПЕДАГОГИЧЕСКО ИЗСЛЕДВАНЕ (ДОКАЗАТЕЛСТВЕНА СТАТИСТИКА).

След представяне на резултатите по описаните начини и определяне на вида на числовото разпределение се преминава към статистическия им анализ. В съответствие с поставената цел на педагогическото изследване, статистическият анализ на установените резултати изисква използването на определени статистически методи. Изборът на конкретния метод е  в зависимост от вида на честотното разпределение, от използваната оценъчна скала и от обема и особеностите на извадката. Тези три фактора налагат използването на параметрични или непараметрични методи. За по-специфични цели на изследването, както и при по-различно разпределение на променливата се прибягва до корелационен, дисперсионен, факторен и др. анализи, чрез които се извеждат връзки и закономерности на изследваните обекти.

Диагностични методи и средства (диагностична процедура:

При този анализ се определят основните характеристики на изследваните методи и средства - обективност, надеждност, валидност и други. По определени методики се изчисляват различни коефициенти, от чиито стойности се прави извод за диагностичните качества на изследваните методи и средства.

Проверка на статистически хипотези:

Този анализ позволява да се направи извод за статистическата значимост на установените резултати и извеждане на връзки и закономерности в изследваните обекти. (21)

3.3.1. ОБРАБОТКА НА ДАННИ ОТ ДИДАКТИЧЕСКИ ТЕСТ (ДИАГНОСТИЧНА ПРОЦЕДУРА).

Дидактическото тестиране е метод на педагогическата диагностика с който се измерват по възможност обективно, надеждно и валидно резултатите от обучението.

Диагностичната процедура включва поредица от дейности, имащи за цел разработка, изследване и оценка на диагностичното средство (дидактически тест) и оценка на състоянието на изследвания обект. Съществен етап в тази процедура е количествената и качествената оценка на установените резултати. На основата на статистически анализ на резултатите от апробирането на теста (пилотно изследване) се определят основните му характеристики (обективност, надеждност, валидност) и качествата на задачите (трудност, дискриминативна сила). Получените данни позволяват да се извърши подобряване на теста.

Резултатите от подобрения вариант са основа за оценка на:

-  състоянието на изследвания обект;

-  постигнатата промяна в обекта на изследването;

-          учениковите постижения.

На основата на качествен анализ на установените резултати се извеждат положителни и отрицателни страни в усвояването на съответното учебно съдържание от учениците, с цел изграждане на стратегия за бъдещо педагогическо въздействие в близък и no-далечен план. (Фиг. 40).

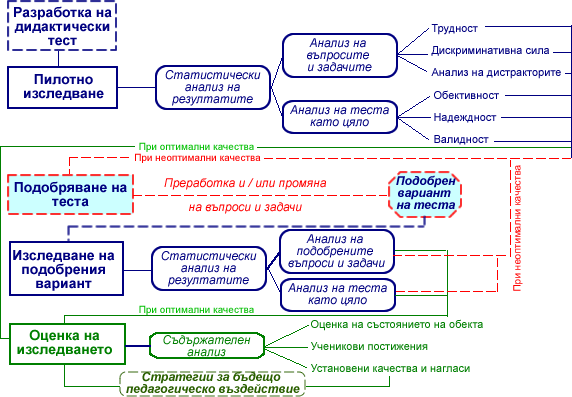
Фиг. 42. Диагностика на дидактическо средство (дидактически тест).

3.3.1.1. АНАЛИЗ НА ТЕСТА КАТО ЦЯЛО.

Основните характеристики на дидактическите тестове са: обективност, надеждност, валидност, сравнимост, икономичност.

а) #Обективността# означава степента на независимост на провеждането и на резултатите от автора на теста. В този случай е необходимо да се определи коефициента на корелация между резултатите от проведения в различни извадки тест.

формула 13 

 като данните се вземат от трите последни колони на честотната таблица (виж Честотна таблица № 1-3)

Друг начин е резултатите от двете групи да се обединят и да се представят като класове от равностойни резултати. Изчисляват се средноаритметичната на така получената извадка и средноквадратичното отклонение. На тяхна база се определя интервала на достоверност. Обективността на теста се определя от отношението:

формула 14

N/n

 където N е броят на статистически достоверните резултати, ап-общият брой на ученици в двете групи.

б) #Надеждността# показва точността на използвания тест. За определяне на надеждността на даден тест се изчислява коефициент на надеждност, който може да има стойности между 0 и 1. Колкото стойността на коефициента е по-близо до 1. толкова надеждността е по-висока. За определяне на този коефициент, който по същество е коефициент на корелация, са известни множество методи (Спирмен - Браун, метод на Рулон, коефициент на Гутман и др.) (6,11,12)

При използване само на един вариант на теста възможно е надеждността да се определи по формулата на Хойт:

формула 15

 

Където:

n е броят на задачите в теста, N - броят на изследваните лица; х -резултатът на съответен ученик и N_R - брой ученици, които са решили съответната задача.

Тази формула се използва, когато е невъзможно тестът да се раздели на две равностойни половинки. Предимството й е, че при нея се използват „суровите" резултати (от първичния протокол), което облекчава обработката.

Когато тестът е проведен в два варианта, или позволява поделяне на равностойни половинки, или е проведен двукратно, удобно е да се ползва коефициентът на Фланаган (г_tt), като преди това се изчисли коефициент за корелация (r_1,2):

формула 16

 

Където:

S₁ - средно квадратично отклонение от първата половина на теста S₂- средно квадратично отклонение от втората половина на теста г_tt - коефициент на корелация между двата варианта или между двете половинки

Например:

При апробацията на дидактически тест, проведена по метода на паралелните тестове, установените резултати от двата варианта на теста и Б) са подложени на групиране и обработка. Изчислените стойности на абсолютната честота са представени в таблица 13.

Таблица 13. Разпределение по честота на резултатите на 24 ученика

Въз основа на честотите са изчислени средните величини и величините на разсейване

Вариант А Вариант Б

X = 9 y = 9

S_x² = 9.478 S_y² = 9.26

S_x = 3.0785 S_y = 3.043

Надеждност на теста , изчислена по формулата на Фланаган:

r_x,y = 0.8 r_1,2 = 0.8

При критериалните тестове надеждността се определя от еквивалентността на тестовите резултати. Използва се коефициентът на Капа-Коуен:

формула 17

където:

N₁ - брой ученици, постигнали целта при първия тест; N₂ - брой ученици постигнали целта при втория тест. Възможно е коефициентът да се изчисли, като се имат предвид резултатите на равностойни половинки от теста.

 в) Валидността на теста показва точността, с която теста мери величините, заложени в целта. Валидността се изследва по пътя на експертните оценки. При педагогическите изследвания се използват критериална, съдържателна и конструктивна валидност, от които по-съществени и по-важни са първите две.

#Критериална валидност# се определя като се пресмята коефициент на корелация между резултатите от теста след експертната му оценка и последователния тест.

Възможно е използването и на т. нар. «Метод на контрастните групи»:

Изчислява се , като се използва формулата:

формула 18

К= 100 - %сл. - %с.

Където: % сл. - процента на тази част от "слабите ученици", които теста определя като изпълнили целта;

%с. - процента на тази част от "силните ученици", които теста определя като неизпълнили целта;

При критериалните тестове, за използването на техниката на контрастните групи е необходимо да се приложат съответните изчислителни техники, доколкото валидността е най-важната характеристика на този тест.

Пример:

 Таблица 14. Честотна таблица на резултатите от Тест I - контрастни групи

Na + Nb          18

V kp = ------------ = --------- = 0.90

n                20

Получената стойност - 0,90 гарантира много добра критериална валидност на теста.

Съдържателна валидност# се определя като среден процент на експертната оценка за хомогенността на задачите и оценката, доколко те покриват учебното съдържание.

Например: За определяне на съдържателната валидност на теста е използвана експертна оценка чрез анкета на 11 експерта. Резултатите от анкетата показват, че 10 от 11 експерти дават положителна оценка на пилотния вариант на теста. По формулата на Лоши, за критериалната валидност  на примерния тест се получава:

   

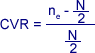
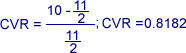
където: п_е - брой на експертите, оценили положително теста; N - общ брой експерти.

При критериалните тестове съдържателната валидност се определя като среден процент от оценката на експертите относно процентът задачи от теста, покриващи целта.

 Конструктна валидност. Като конструкти могат да служат интелигентността на учениците, способността им да прилагат специфични умения и т.н. Тя се определя като корелация между резултатите от всяка задача и резултатите от теста като цяло.

 3.3.1.2.  АНАЛИЗ НА ЗАДАЧИТЕ

Ако тестът притежава описаните основни характеристики необходимо е той да се изпробва (ако не е готов, стандартизиран тест), като се извърши апостериорен анализ. С други думи, след решаване на теста получените данни се подлагат на специални процедури, като анализът се извършва по отношение на следните характеристики на тестовите задачи: анализ на трудността, анализ на дискриминативната сила, анализ на дистракторите.

`

#Анализ на трудността#.

Трудността на дадена тестова задача се представя чрез индекса на трудност:

формула 19

където: N_R - брой на учениците, решили вярно задачата; N - общ брой ученици, решавали същата задача. Ако индексът на трудност е много нисък като стойност, това означава, че задачата следва да се промени, като се цели нейното олекотяване.

#Анализ на дискриминативната сила#.

Дискриминативната сила на дадена задача показва възможността й да разграничи силните от слабите по постижения ученици. Коефициентът варира между -1 и +1.

Най-използваната формула за пресмятане на дискриминативната сила е:

формула 20

Където:

R_U - брой на учениците от «силната» група решили задачата R_L- брой на учениците от «слабата група» решили задачата T - общ брой на учениците решавали задачата

#Анализ на дистракторите#.

Най-общо, понятието «дистрактор» означава «грешен отговор». При определянето на качествата на дистракторите се използват понятията «силна» и «слаба» група. Определянето на състава на тези групи се прави или на база предварителните (предхождащи изследването) резултати на учениците, или като се имат предвид показаните в хода на изследването резултати, под и над средноаритметичната на разпределението.

Според Берк основните критерии при анализа на дистракторите са следните:

а) Всеки дистрактор да бъде посочен от повече «слаби» отколкото
«силни» ученици.

б) Всеки дистрактор да се посочва от поне един «силен» ученик.

в) В силната група, броят на учениците, избрали дистрактор да не
надвишава броя на тези, посочили верен отговор.(6,11,12)

3.3.2. ПРОВЕРКА НА СТАТИСТИЧЕСКИ ХИПОТЕЗИ.

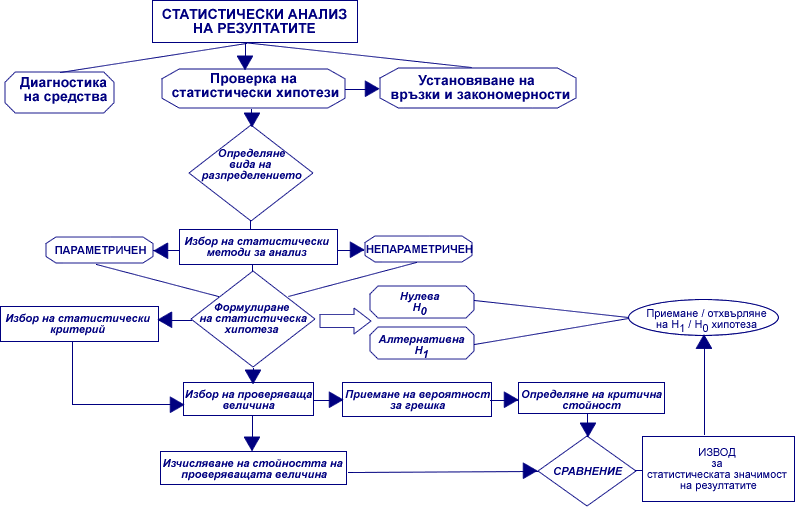
Определянето на статистическата значимост на резултатите разкрива тяхната закономерност или случайност. Този анализ дава отговор на въпроса, доколко установената разлика между вариантите се дължи на приложеното педагогическо въздействие или е резултат от случайни фактори. Този анализ е свързан с проверка на статистически хипотези, при което се преминава през няколко етапа (Фиг. 43).

Фиг. 43 Етапи на статистическия анализ на резултати от педагогическо изследване.

Параметричните методи се прилагат при нормално разпределение на променливата. Те изискват данни измерени предимно с интервална оценъчна скала и са силни при изследване на средни или големи извадки. Основни параметрични методи са тестът на Стюдънт (Т), тестът на Фишер (F) и др.

Непараметричните методи се прилагат, когато не е известен вида на разпределението на променливата. Чрез тях се анализират всички видове данни, независимо от оценъчната скала. Тяхната сила е при изследване на малки извадки. Основни непараметрични методи са х² (хи-квадрат), Критерий на Фишер, Знаков критерий ...(14,21)

Формулировка на статистическа хипотеза. #Статистическата хипотеза# представлява предположение относно формата или параметрите на една или на повече случайни величини, което може да се провери по статистически път, т.е. по данните от представителни извадки. В статистиката строго са обособени два вида статистически хипотези -нулева и алтернативна. Нулевата хипотеза (Н₀) гласи, че изследваната извадка принадлежи на генералната съвкупност. Алтернативната хипотеза (Н₁) гласи, че извадката не принадлежи на генералната съвкупност. Тя всъщност отрича нулевата. Алтернативната хипотеза изразява предположенията, формулирани в хипотезата на изследването.

Приемането, на която и да е от двете хипотези, е свързано с определен риск. Съществуват две възможности за допускане на грешки - грешки от първи род - свързани са с отхвърлянето на нулевата хипотеза, като тя в действителност е вярна; грешки от втори род - допускат се като се потвърди нулевата хипотеза, а в същност е вярна някоя от алтернативните хипотези.

 Избор на статистически критерий и проверяваща величина. Всеки конкретен статистически метод борави с определен, характерен за него критерий и величина, която се изчислява по определен начин. В критерия се съдържа условието, при което проверяваната статистическа хипотеза трябва да се приеме или отхвърли.

 Изчисляване стойността на проверяващата величина. Всеки метод изисква, на основата на реално установените резултати, по описани правила и формули, да се изчисли стойността на проверяващата величина.

Определяне вероятността за грешка. Както при всяко измерване, а и в статистиката се приема определено ниво на значимост, определена вероятност за грешка при извеждане на заключенията от проведеното изследване. В педагогическите изследвания се използва обикновено вероятност за грешка 0,05 или 5 %. Това означава, че сигурността на направените изводи е 95 %.

 Определяне критичната стойност на проверяващата величина. Всеки статистически метод се базира на определена закономерност. В съответствие с нея са определени теоретичните стойности на проверяващата величина в зависимост от вероятността за грешка - степени свобода. Критичната стойност се взема от таблици.

- ако емпиричната характеристика е по-голяма от теоретичната, следва да се отхвърли нулевата хипотеза в полза на алтернативната;

- ако емпиричната характеристика е равна или по-малка от теоретичната, нулевата хипотеза не може да бъде отхвърлена.

 Сравнението на табличната с реално изчислената стойност на проверяващата величина позволява да се вземе решение за приемането или отхвърлянето на нулевата статистическа хипотеза. Това е заключителният етап, който е свързан с обосноваването на конкретно решение:

Ако се приеме нулевата хипотеза, това означава, че установените разлики в резултатите на двата варианта не са статистически значими. Постигнатите положителни промени се дължат не само на реализираното целенасочено педагогическо въздействие, те са резултат и от случайни фактори.

Ако   се   отхвърли   нулевата   и   се   приеме алтернативната хипотеза, това означава, че установените разлики в резултатите на двата варианта са статистически значими. Постигнатите положителни промени се дължат на реализираното целенасочено педагогическо въздействие. Въздействието на случайните фактори е в границите на приетата вероятност за грешка - 5 %. Статистическите критерии за проверка на хипотези зависят от начина на дефиниране на алтернативната хипотеза, от избрания метод на проверка и от равнището на значимост.

Степените на свобода се използват като координати при намиране на теоретичната стойност на характеристиката. Те зависят от обема на извадката и от броя на ограничителните условия, които са възприети при провеждането на анализа.

 Изложената последователност на работа при проверката на хипотези може да се приложи при решаването на различни практически задачи, които възникват при педагогическите изследвания и се отнасят до величини, имащи формата на средноаритметична и дисперсия.

1.       U - критерий за сравняване на средни стойности:

                H₀: m₁=m₂; H₁: m₁≠m₂

          С m₁ и m₂ са означени средните аритметични величини на сравняваните разпределения; с x_i – измерените в извадките

        Приема се ниво на значимост 0,05 или 5%

        Формула за изчисляване на критерия:

 Формула 21

където: n₁, n₂ - обем на двете извадки; S₁²,S₂²  - дисперсии

Стойност на проверяващата величина при a= 0,05 - g

Ако  |U| <  Ua приема се Н₀; Ако  |U| ≥  Ua приема се H₁

2. F - критерий за сравняване на дисперсии:

H₀:S₁²=S₂²; H₁: S₁²≠S₂²

С S₁² и S₂² са означени дисперсиите на сравняваните
разпределения

Приема се ниво на значимост 0,05 или 5%

Формула за изчисляване на критерия:

Формула 22

Ако F < Fa приема се H₀; Ако F≥Fa приема се H₁

3. #Корелационен анализ#:

Позволява да се установи наличието на връзка между две или повече променливи и да се оцени степента на зависимост между тях. Корелационният анализ преминава през следните етапи:

1.  Предварително изучаване на взаимовръзката (графично);

2.  Изследване на двойни зависимости;

3.  Изследване на множествени (многофакторни) зависимости.

степента на зависимост (силата на връзката) между променливите се изразява чрез коефициент на корелация. В зависимост от използваните скали за отчитане на корелиращите данни се използват различни начини на изчисляване на коефициента на корелация.

• Рангова корелация (Корелационен коефициент на Пиърсън-Браве - r) Използва се при данни сканирани в интервална и абсолютна скала:

 Формула 23

• Корелация при качествени белези (Корелационен коефициент на Крюгер-Спирмън - R) Използва се при данни скалирани в ординална скала:

Формула 24

 Корелация при качествени белези (Тетрахоричен корелационен коефициент - г_tet ) Използва се при данни скалирани в номинална скала:

Формула 25

a,b,c,d - съдържание на клетките в таблица "четири полета".

Когато данните са скалирани ординално при едната величина и интервално в другата могат да се изчислят съответно коефициенти на бисериална корелация (r_bis) и точково-бисериална корелация (r_pbis)

Всички посочени коефициенти приемат стойност от +1 до -1. Стойност "0" означава съответно липса на връзка.

При интерпретирането на получените в следствие на корелационният анализ данни, задължително следва да се има предвид, че наличието на корелация не означава каузалност (причинна връзка), а  тенденция. Дори и при установена корелация между две величини не може да се определи коя от тях предопределя другата.

 4. #Регресионен анализ#:

Регресионният анализ дава оценка на стойността на една случайна променлива въз основа на знанията ни за друга променлива. По същество се свежда до установяване на най-подходящия аналитичен израз на съответната функционална зависимост, чрез която се представя най-адекватно проявената корелационна зависимост. По-образно, той дава отговор на въпроса "какъв е характера на зависимостта". За да се определи този "характер" е необходимо първо да се установи наличието на корелационна връзка. Това означава, че първо трябва да се извърши корелационен анализ. Следователно регресионният анализ следва корелационния.

Чрез регресионният анализ се решават няколко типа задачи:

- Установяване фактите за изменчивост на интересуващото ни явление.

- Установяване обективното съществуване на зависимост между две или повече интересуващи ни явления.

- Изследване формата, моделът на установената корелационна зависимост.

- Измерване на конкретните количествени съотношения и факторни влияния между взаимно свързаните явления.

- Оценяване степента на влияние на факторите върху зависимата променлива чрез определяне значимостта на коефициента на регресия.

За решаването на тези задачи се използват различни методи. В зависимост от броя на включените фактори, регресионните методи могат да бъдат еднофакторни или многофакторни. В зависимост от вида на използваната функция се разделят на праволинейни и криволинейни.

 5. #Дисперсионен анализ.#

По своята същност дисперсионният анализ е метод за статистическа проверка на хипотези. Чрез него може да се изследва дали съществува закономерна статистически значима връзка и зависимост между две или повече явления. Основава се на оценката на дисперсията на изследваната съвкупност без влиянието на даден фактор и след неговото въздействие. Ако двете дисперсии са равни, то връзка между този фактор и изследваното явления няма и обратно - ако дисперсиите са различни то съществува връзка между фактора и настъпилото изменение в явлението. За оценка на статистическата значимост на установената разлика в дисперсиите се използва F - критерия на Фишер.

В зависимост от включените в анализа фактори, дисперсионният анализ се разглежда като еднофакторен, двуфакторен и многофакторен. Най-често в педагогическите изследвания, особено при разработването на дипломни работи, се използва еднофакторния дисперсионен анализ. Чрез него се проверяват статистически хипотези, че средните значения на две или повече извадки са еднакви, че извадките принадлежат към една и съща генерална съвкупност.

6. #Тренд-анализ.#

Анализ на тренда се прилага, когато са установени данни за динамиката на определен фактор (установени значения на Y и установени значения на X). Той позволява да се предвиди развитието на този фактор в бъдеще (да се предвидят нови значения за X). Има определено място при прогностичните изследвания. Резултатите от изследването се използват за създаване на математически модел на процеса. На основата на този модел се извършват по-нататък и прогнозите за влиянието на изследвания фактор.

 7. #Факторен анализ. #

Факторният анализ е метод за многомерен статистически анализ на вариациите на признаците, позволяващ да се открият скрити, външно ненаблюдаеми техни комбинации и закономерности на връзката им, както и за откриване на влиянието на скрити фактори върху изучавания обект.

Целта на факторния анализ е да се потърси потвърждение на най-простата хипотеза за факторите, определящи взаимовръзката между наблюдаваните променливи, както и да се разкрие структурата на някакво сложно явление, което в изследването е резултативен признак.

8. #Клъстър-анализ. #

Клъстър анализът е многомерен анализ и позволява да се осъществи класификация на данните едновременно по няколко признака. Известен е още като таксономия. Прилага се при отсъствие на предварителна информация за групирането на данните. Самото групиране става по такъв начин, че някои елементи в някакъв смисъл са по-близки един с друг в сравнение с останалите. Целта на изследването чрез този анализ е да се открият групите от променливи без разкриване на факторите, обясняващи връзките между тях.(20,28)

3.3.3. АНАЛИЗ НА ДАННИ ОТ АНКЕТНИ ПРОУЧВАНИЯ

При количественият анализ на анкетни данни е важно, разработващият анкетата да е заложил предварително в нейната структура и методите за анализ – при подбора на типа и структурата на въпросите и отговорите.

3.3.3.1. Z – тест - може да се използва безразлично какъв е обемът на извадките.

1. Изчисляват се относителните честоти на отговорилите по един и същ начин на даден въпрос от двете извадки (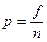), където f е броят на отговорилите по проверявания начин на дадения въпрос, а n  е обемът на извадката). Означават се съответно с p₁ и p₂.

2. Формулират се нулева и алтернативна хипотези:

Н₀: Разликата в относителните честоти между двете извадки не е статистически значима, т.е. тя се дължи на случайни фактори.

Н_а: Разликата в относителните честоти между двете извадки е статистически значима, т.е. тя се дължи на влиянието на изследвания фактор.

3. Пресмята се проверяващата величина z по формулата:

Формула 26

където n₁ и n₂ са обемите на двете извадки.

При вероятност за грешка α = 0.05 “критичната” стойност за z е z_α = 1.96. Ако z < z_α нулевата хипотеза се приема, т.е. с 95 % вероятност можем да приемем, че не съществува статистически значима разлика между становищата на двете групи анкетирани по дадения проблем лица.

3.3.3.2. Тест на Ван Дер Веерден - приложим при малки и средни извадки с обем до 200 респонденти):

Извадките се обединяват в една и се пресмятат общите абсолютна и относителна честота на варианта на отговор на съответния въпрос от анкетата:

където 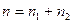 е общият обем изследвани лица от двете групи. Другите означения са както при z – теста. Относителните честоти се изчисляват в проценти. Пресмята се величината s² :

Формула 27

Ако , то се приема нулевата хипотеза.

4.3.3.3. Тест на Лудвиг - за извадки с голям обем - над 200 д.

 Пресмята се величината ε_α по формулата:

Формула 28

Относителните честоти са изчислени както при z – теста.

Пресмята се проверяващата величина t по формулата:

(Означенията имат същото значение, както при посочените тестове.)

“Критичната” стойност t_α,ν се взема от таблица като α = 5 %, а ν = n₁ + n₂ -2.

Ако t < t_{α, ν} , то нулевата хипотеза се приема.

333.3.4. КАЧЕСТВЕН АНАЛИЗ НА РЕЗУЛТAТИ ОТ  ПЕДАГОГИЧЕСКИ ИЗСЛЕДВАНИЯ

Емпиричните резултати от всяко педагогическо изследване позволяват както количествен, така и качествен анализ. При това двата анализа трябва да се разглеждат в тяхното неразчленимо единство.

Разгледаните до тук методи на статистическия (количествен) анализ дават различни възможности за доказване достоверността на получените резултати, значимостта на установените различия между изследваните варианти, наличието на връзки и закономерности и др. достоверността и значимостта на данните, установеното наличие на връзки са резултативни факти, но те не дават обяснение на установените изменения в изучаваните обекти. Поради това, при всяко педагогическо изследване е необходимо да се осъществи и качествен анализ на установените резултати: да се установи какво е значението на данните от изследването за решаването на научните въпроси; да се съотнесат изводите т статистическия анализ към целите и хипотезата на изследването, като е анализират и обяснят всички факти, които противоречат на хипотезата; а се потърси съгласуваност с теоретичните постановки в изследваната област и др. Този целенасочен качествен анализ, търсенето на обяснение а резултатите от педагогическото изследване се извършва чрез емпиричен теоретичен анализ. Това са две възможни направления и същевременно основни етапи на един цялостен процес. (Фиг. 44).

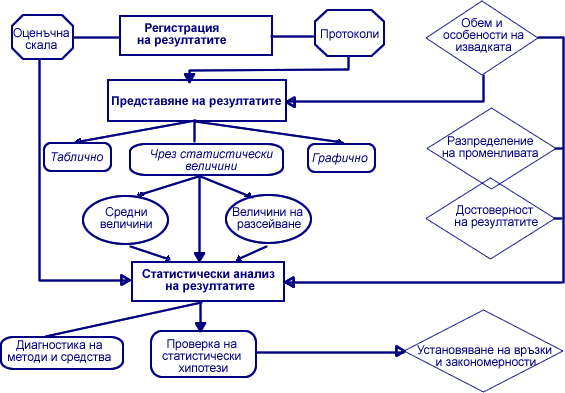
Фиг. 44 Анализ и обяснение на резултати от педагогически експеримент.

Емпиричният анализ има за основна цел съотнасяне на установените резултати от статистическия анализ към целите и хипотезите на изследването. Това изисква от една страна да се опишат наблюдаваните изменения и установените връзки и закономерности в изследваните явления и процеси, а от друга - да се търсят вероятните причини за тези изменения и закономерности. В тази насока емпиричният анализ се осъществява на две взаимно свързани равнища като описателен и каузален (причинно-следствен) анализ.

Теоретичният анализ е насочен към установяване степента на съгласуване на получените резултати и изводи с позициите на определени теоретични схващания по проблема на изследването.(7)

3.3.4.1. ОПИСАТЕЛЕН АНАЛИЗ

Педагогическите явления и процеси са взаимосвързани и задължително се разглеждат в комплекс. Задълбоченото им изучаване, вследствие на наблюдаваните в тях изменения предполага преди всичко точно описание и последващо обяснение.

Описателният анализ се прави на основата на конкретни количествени данни. Следователно разсъжденията и изводите трябва да се подкрепят и да се илюстрират с тези фактически данни - числов материал, таблици, графики. Описанието и обяснението изискват да се използват ясни, точно определени понятия и термини.

Описателният анализ на емпиричния материал се осъществява в няколко насоки:

Класификация на данните - извеждане на общото и различното между белезите, чертите, особеностите на процесите и явленията. Целта е подреждането на особеностите в групи и категории и оформяне на характеристика на частното, произтичаща от общото.

Описание на данните - достигане до характеристика на явлението откъм неговата феноменологична страна, но с оглед на отношението му към други явления. Това налага търсене на подобие, разлики, зависимости.

Генетично описание - описание на развитието на изучавания процес.

Структурно описание - разкриване на строежа, взаимовръзката между частите и цялото, между отделни параметри в определен момент.

Структурно-генетично описание - изучаване на изменението на структурата във времето.

Описателният анализ обобщава данните и дава отговор на редица въпроси: кое допълнително въздействие е оказало най-силно влияние за наблюдаваното изменение; как се подреждат според силата на влиянието си отделните социално-педагогически фактори; какво е необходимо да се осъществи в по-нататъшната работа и т.н.

Колкото и точно и задълбочено да се осъществи едно описание, то засяга само наблюдаваното явление, но не и неговата същност. Но на основата на описателния анализ може да се осъществи по-нататъшна оценка на проведеното педагогическо изследване.

Изведените закономерности в изследвания обект не могат да се докажат на основата на описателния анализ. Резултатите от него са база за осъществяване на другия емпиричен анализ - каузалния.

3.3.4.2. КАУЗАЛЕН АНАЛИЗ

Каузалният (причинно-следствен) анализ има за цел разкриване та причините за настъпилите промени в зависимата променлива и за получаването именно на тези, а не на други резултати. Този анализ трябва да даде отговор на въпроса "Защо” по-конкретно „от какво” зависят получените резултати. Дали са вследствие на приложеното допълнително въздействие (приложената методика) или са резултат и от други фактори.

Изводите на каузалния анализ се аргументират с емпиричните резултатите от изследването, както при описателния анализ, но тук вече се налага да се използват и статистически величини - средноаритметични  величини на разсейване. Освен това се основава на фиксираната динамика в развитието, установените връзки и зависимости в изследваното явление.

Същността на каузалния анализ се изразява в разкриването на причинно-следствените връзки между изследваните явления и процеси. Причинно-следствени връзки между две явления се търсят тогава, когато :е предполага, че изменението на едното предизвиква съпътстващо или последващо изменение на другото.

Каузалните (причинно следствени) връзки се делят на: постоянни, регулярни, монотонни и инвариантни; силни и слаби; универсални и частни; преки (непосредствени) и косвени; положителни и отрицателни препятстващи); основни и допълнителни, (по 20)

Силата на каузалния анализ е в определянето на безусловните и условните връзки. (16) Безусловната каузална връзка се характеризира с думите "винаги" и "никога", а условната - с "при условие".

Безусловната връзка може да е в позитивна и негативна форма.

Като позитивна безусловна връзка може да се охарактеризира тази връзка, при която практически се установява, че винаги след причината А следва следствието В.

Като негативна безусловна връзка може да се охарактеризира тази връзка, при която практически се установява, че А е винаги и навсякъде е необходимо условие за В. (По 20)

Условната връзка е такава връзка, която позволява да се тълкува като причинна в случаите, когато няма основание да се говори за безусловна причинност, но е установена статистическа връзка (корелация). (Пак там)

При изследване на педагогически явления (променливи) най-често се установява влияние на един или на няколко неизвестни или допълнителни фактора. Между тях може да съществува каузална връзка, но е възможно всеки от тях да оказва влияние, независимо от другите. Именно това са най-често срещаните връзки в педагогическите изследвания, при което се говори за сложна условна причинност. Тази сложна постановка изисква да се търси не една, а няколко причини и произтичащите от тях следствия. При установяване на такава ситуация се налага всяко явление да се разглежда в три аспекта - като причина, като следствие и като условие.

3.3.4.3. ТЕОРЕТИЧЕН АНАЛИЗ

Педагогическите изследвания, както вече подчертахме имат предимно теоретико-емпиричен характер. Това налага направеният емпиричен анализ да се разшири и допълни и с теоретичен. Същността на теоретичния анализ се изразява в разглеждане на установените по емпиричен път резултати и изводи от позициите на определени теоретични постановки. Насоката на анализа е степента на съгласуване на емпиричните резултати с теоретичните схващания по изследвания проблем. При това. на изход от анализа, се достигало един от възможните три варианти:

1. Получените емпирични данни се съгласуват с теорията. При това данните могат да:

-   препотвърждават теорията;

-   конкретизират отделни страни на приложението й;

-   разширяват обхвата на теорията.

2.        Получените данни само частично се съгласуват с теорията. При такава ситуация:

- причината може да се търси в подхода и методиката на провеждане на изследването;

- ако изследването е коректно проведено, то би следвало да се търси форма за изменение на теорията;

- данните  могат  да  послужат  за  развиване  и усъвършенстване на теорията в определено направление.

3. Получените данни не се съгласуват с теорията. Изводите при това са:

- ако изследването е коректно, следва че теорията влиза в противоречие с нови факти;

- възниква необходимост от разработка на нова теория.

Това са три основни случаи, които трудно ще срещнем в чист вид. Но всяко емпирично изследване в някаква степен спомага за движението, изменението и развитието на теорията в изследваната област.

Направените констатации по отношение на съгласуваността на лиричните данни с теоретичните постановка в дадена област са само първия етап от теоретичния анализ. Следва анализът да се задълбочи в посока на обогатяване на педагогическото познание, което може да се изрази в:

-   усъвършенстване на системата от теоретични съждения със закономерен характер;

-   изясняване на понятията и термините, като основни елементи теорията;

-  доказване практическото приложение на определена теория. Теоретичният и емпиричният анализ са в пълно съответствие с двете  взаимосвързани страни (емпирична и теоретична) на единния изследователски процес, които взаимно се предполагат и съществуват в единство.

КЛЮЧОВИ ПОНЯТИЯ ПО ТЕМАТА:

абсолютна честота; анализ на трудността; анализ на дискриминативната сила; анализ на дистракторите; валидност; валидност, критериална; валидност, съдържателна; вариационен ред; величини на разсейване; дисперсия; дисперсионен анализ; извадка; интервална скала; клас; клъстър-анализ; корелационен анализ; кръгова диаграма; медиана; мода; надеждност; натрупана честота; номинална скала; обективност; полигон; първичен протокол; (още, таблица на значенията) рангова скала; регресионен анализ; среда на класа; средни величини; статистическа хипотеза; стълбчеста диаграма; средноаритметична на вариационния ред; средноаритметична на разпределението; средно квадратично отклонение; тренд-анализ; факторен анализ; хистограма; ширина на класа.

 

 

ВЪПРОСИ, ЗАДАЧИ И кАЗУСИ за самоподготовка:

ЗАДАЧА 1. Опишете конструирането на извадка за педагогическо изследване:

Вариант А. Анкетиране на учениците от началния етап на основната образователна степен от Старозагорска област.

 

Вариант Б. Диагностика на резултатите от обучението по Астрономия  на учениците от Старозагорска област.

АНАЛИЗ НА ДИАГНОСТИЧНО СРЕДСТВО:

А. ОПРЕДЕЛЯНЕ КАЧЕСТВАТА НА ЗАДАЧИТЕ В ДИДАКТИЧЕСКИ ТЕСТ

ЗАДАЧА 2. По дадените данни в таблицата определете характеристиките на задачите – трудност и дискриминативна сила. Направете съответните изводи и вземете решение за коригиране или отхвърляне на конкретни задачи.

В първата колона са подредени в низходящ ред постигнатите резултати на учениците.

Силна група: Първите 10 тестирани с по-високите резултати (от № 1 – до № 10)

Слаба група:  Вторите 10 тестирани с по-ниските резултати (от № 11 – до № 20)

Трудност. Определя се коефициент на трудност (Р) в проценти.

Оптимални граници на коефициента:  30 < P < 70.

При стойност на коефициента:

• под 30 % и над 70 % - препоръчително е задачата да се преработи;
• под 20 % и над 80 % – препоръчително е задачата да се подмени.

Дискриминативна сила. Определя се индекс на разграничителна сила (DP) в проценти.

Оптимални граници на индекса: 40 < DP < 60.

При стойност на индекса:

- под 30 % и над 70 % – препоръчително е задачата да се подмени.